
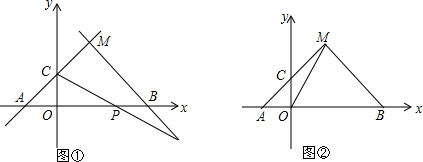
分析 (1)根据直线y=x+1交x轴于点A,交y轴于点C,得到A(-1,0),C(0,1),进而得到点B(3,0),过点M作ME⊥y轴于点E,证明△AOC≌△MEC,
所以EM=AO=1,EC=OC=1,所以点M的坐标为(1,2),设直线BM的解析式为y=kx+b,把点M的坐标为(1,2),点B(3,0)代入y=kx+b得:$\left\{\begin{array}{l}{k+b=2}\\{3k+b=0}\end{array}\right.$,即可解答;
(2)根据点N在直线直线y=-x+3上,设点N的坐标为(x,-x+3),根据BN=AC,求出点N的坐标为(4,-1),设直线NC的解析式为y=mx+n,把点N的坐标为(4,-1),C(0,1)代入y=mx+n得:$\left\{\begin{array}{l}{4m+n=-1}\\{n=1}\end{array}\right.$,所以直线NC的解析式为y=-$\frac{1}{2}$x+1,当y=0时,x=2,所以点P的坐标为(2,0).
(3)①当K在线段BM上时,根据M点坐标为(1,2),得到直线OM的方程为:y=2x.因为直线OM的斜率大于直线y=x的斜率,所以在MB上存在点K点使∠MOK=45°,设直线OM的斜率为k2,直线OK的斜率为k1,设k点坐标为(a,b),则k2=2,${k}_{1}=\frac{b}{a}$,再根据两直线夹角公式tanx=$\frac{{k}_{2}-{k}_{1}}{1+{k}_{2}{k}_{1}}$,得:tan45°=$\frac{2-\frac{b}{a}}{1+2•\frac{b}{a}}$=1,整理得:a-3b=0,根据直线MB方程为y=-x+3,点K在MB上,得到b=-a+3,联立$\left\{\begin{array}{l}{a-3b=0}\\{b=-a+3}\end{array}\right.$,求出a,b,即可解答.②当K在BM的延长线上时,∵∠K′OM=45°,∠MOK=45°,推出OK⊥OK′,由直线OK的解析式为y=$\frac{1}{3}$x,推出直线OK′的解析式为y=-3x,利用方程组求出点K′坐标即可;
解答 解:(1)∵直线y=x+1交x轴于点A,交y轴于点C,
∴A(-1,0),C(0,1),
∴OA=OC=1,
∵OB=3OA,
∴OB=3,
∴点B(3,0),
如图①,过点M作ME⊥y轴于点E,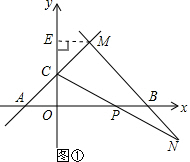
∵OA=OC,
∴∠CAO=∠OCA=45°,
∴∠ACO=∠ECM=45°,
∵AC=CM,
∴△AOC≌△MEC,
∴EM=AO=1,EC=OC=1,
∴点M的坐标为(1,2),
设直线BM的解析式为y=kx+b,
把点M的坐标为(1,2),点B(3,0)代入y=kx+b得:
$\left\{\begin{array}{l}{k+b=2}\\{3k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$,
∴直线BM的解析式为:y=-x+3.
(2)∵点N在直线直线y=-x+3上,
∴设点N的坐标为(x,-x+3),
∵BN=AC,
∴$\sqrt{{(x-3)}^{2}+(-x+3)^{2}}=\sqrt{{1}^{2}+{1}^{2}}$,
解得:x1=4,x2=2,
∵点N在MB的延长线上,
∴x>3,
∴x=4,
∴点N的坐标为(4,-1),
设直线NC的解析式为y=mx+n,
把点N的坐标为(4,-1),C(0,1)代入y=mx+n得:
$\left\{\begin{array}{l}{4m+n=-1}\\{n=1}\end{array}\right.$
解得:$\left\{\begin{array}{l}{m=-\frac{1}{2}}\\{n=1}\end{array}\right.$
∴直线NC的解析式为y=-$\frac{1}{2}$x+1,
当y=0时,x=2,
∴点P的坐标为(2,0).
(3)如图②,①当K在线段BM上时,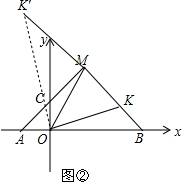
∵M点坐标为(1,2),
∴直线OM的方程为:y=2x.
∵直线OM的斜率大于直线y=x的斜率,
∴在MB上存在点K点使∠MOK=45°,
设直线OM的斜率为k2,直线OK的斜率为k1,
设点K坐标为(a,b),
则k2=2,${k}_{1}=\frac{b}{a}$,
再根据两直线夹角公式tanx=$\frac{{k}_{2}-{k}_{1}}{1+{k}_{2}{k}_{1}}$,
得:tan45°=$\frac{2-\frac{b}{a}}{1+2•\frac{b}{a}}$=1,
整理得:a-3b=0,
∵直线MB方程为y=-x+3,点K在MB上,
∴b=-a+3,
联立$\left\{\begin{array}{l}{a-3b=0}\\{b=-a+3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{9}{4}}\\{b=\frac{3}{4}}\end{array}\right.$,
∴K点的坐标为($\frac{9}{4}$,$\frac{3}{4}$).
②当K在BM的延长线上时,∵∠K′OM=45°,∠MOK=45°,
∴OK⊥OK′,
∵直线OK的解析式为y=$\frac{1}{3}$x,
∴直线OK′的解析式为y=-3x,
由$\left\{\begin{array}{l}{y=-3x}\\{y=-x+3}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=\frac{9}{2}}\end{array}\right.$,
∴K′(-$\frac{3}{2}$,$\frac{9}{2}$).
综上所述,满足条件的点K的坐标为($\frac{9}{4}$,$\frac{3}{4}$)或(-$\frac{3}{2}$,$\frac{9}{2}$)
点评 本题考查了一次函数、全等三角形的性质与判定、勾股定理,解决本题的关键是用待定系数法求一次函数的解析式,在(3)中,根据直线的斜率判定点K的存在是关键,并注意数形结合思想的应用.


科目:初中数学 来源: 题型:选择题
| A. | x3-x=x(x-1) | B. | x2-y2=(x-y)2 | ||
| C. | -4x2+9y2=(2x+3y)(2x-3y) | D. | x2+6x+9=(x+3)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 收费方式 | 月使用费/元 | 包时上网时间/h | 超时费/(元/min) |
| A | 30 | 25 | 0.05 |
| B | 50 | 50 | 0.05 |
| C | 120 | 不限时 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
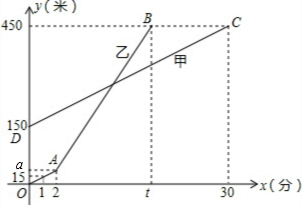 甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,请根据图象提供的信息解答下列问题:
甲乙两人同时登山,甲、乙两人距地面的高度y(米)与登山时间x(分)之间的函数图象如图所示,请根据图象提供的信息解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com