
分析 进行分式的乘、除、乘方混合运算时,应先把各个分式进行乘方运算,再进行分式的乘除运算,即“先乘方,再乘除”,首先求出($\frac{-xy}{z}$)3、($\frac{yz}{-x}$)2的值各是多少,然后从左向右依次计算,求出算式($\frac{-xy}{z}$)3•(-$\frac{xz}{y}$)÷($\frac{yz}{-x}$)2的值是多少即可.
解答 解:($\frac{-xy}{z}$)3•(-$\frac{xz}{y}$)÷($\frac{yz}{-x}$)2
=$(-\frac{{{x}^{3}y}^{3}}{{z}^{3}})•(-\frac{xz}{y})÷\frac{{{y}^{2}z}^{2}}{{x}^{2}}$
=$\frac{{{x}^{4}y}^{2}}{{z}^{2}}÷\frac{{{y}^{2}z}^{2}}{{x}^{2}}$
=$\frac{{x}^{6}}{{z}^{4}}$
故答案为:$\frac{{x}^{6}}{{z}^{4}}$.
点评 此题主要考查了分式的乘除法的运算方法,要熟练掌握,解答此题的关键是要明确:进行分式的乘、除、乘方混合运算时,应先把各个分式进行乘方运算,再进行分式的乘除运算,即“先乘方,再乘除”.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
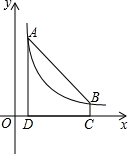 如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com