
����Ŀ����ͼ����Rt��ABC�У���B��90�㣬AC��60cm����A��60�㣬��D�ӵ�C������CA������4cm/s���ٶ����A�����˶���ͬʱ��E�ӵ�A������AB������2cm/s���ٶ����B�����˶���������һ���㵽���յ�ʱ����һ����Ҳ��ֹ֮ͣ�˶������D��E�˶���ʱ����ts������D��DF��BC�ڵ�F������DE��EF��
��1����֤��AE��DF��
��2���ı���AEFD�ܹ���Ϊ����������ܣ������Ӧ��tֵ��������ܣ���˵�����ɣ�
��3����tΪ��ֵʱ����DEFΪֱ�������Σ���˵�����ɣ�
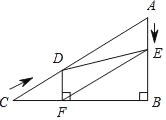
���𰸡���1�������������2����t��10ʱ��AEFD�����Σ���3����t��![]() ʱ����DEF��ֱ�������Σ���EDF��90�㣩����t��12ʱ����DEF��ֱ�������Σ���DEF��90�㣩��
ʱ����DEF��ֱ�������Σ���EDF��90�㣩����t��12ʱ����DEF��ֱ�������Σ���DEF��90�㣩��
��������
��1����Rt��ABC�У�������֪���������C��30�����������֪CD��4tcm��AE��2tcm����ֱ����CDF�У�����30���ֱ�������ε����ʿɵ�DF��![]() CD��2tcm���ɴ˼���֤��DF��AE����2����DF��AB��DF��AE������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��οɵ��ı���AEFD��ƽ���ı��Σ���AD��AEʱ���ı���AEFD�����Σ����ɵ�60��4t��2t�����t��10������t��10ʱ��AEFD�����Σ���2���ܣ�����EDF��90������DEF��90�����������t��ֵ���ɣ�
CD��2tcm���ɴ˼���֤��DF��AE����2����DF��AB��DF��AE������һ��Ա�ƽ������ȵ��ı�����ƽ���ı��οɵ��ı���AEFD��ƽ���ı��Σ���AD��AEʱ���ı���AEFD�����Σ����ɵ�60��4t��2t�����t��10������t��10ʱ��AEFD�����Σ���2���ܣ�����EDF��90������DEF��90�����������t��ֵ���ɣ�
��1��֤��������Rt��ABC�У���B��90�㣬AC��60cm����A��60�㣬
���C��90�㩁��A��30�㣮
�������֪��CD��4tcm��AE��2tcm��
�֡���ֱ�ǡ�CDF�У���C��30�㣬
��DF��![]() CD��2tcm��
CD��2tcm��
��DF��AE��
��2����DF��AB��DF��AE��
���ı���AEFD��ƽ���ı��Σ�
��AD��AEʱ���ı���AEFD�����Σ�
��60��4t��2t��
��ã�t��10��
����t��10ʱ��AEFD�����Σ�

��3����t��![]() ʱ��DEF��ֱ�������Σ���EDF��90�㣩����t��12ʱ����DEF��ֱ�������Σ���DEF��90�㣩��
ʱ��DEF��ֱ�������Σ���EDF��90�㣩����t��12ʱ����DEF��ֱ�������Σ���DEF��90�㣩��
�������£�
����EDF��90��ʱ��DE��BC��
���ADE����C��30��
��AD��2AE
��CD��4tcm��
��DF��AE��2tcm��
��AD��2AE��4tcm��
��4t+4t��60��
��t��![]() ʱ����EDF��90�㣮
ʱ����EDF��90�㣮
����DEF��90��ʱ��DE��EF��
���ı���AEFD��ƽ���ı��Σ�
��AD��EF��
��DE��AD��
���ADE��ֱ�������Σ���ADE��90�㣬
�ߡ�A��60�㣬
���DEA��30�㣬
��AD��![]() AE��
AE��
AD��AC��CD��60��4t��cm����AE��DF��![]() CD��
CD��
��60��4t��t��
���t��12��
������������t��![]() ʱ��DEF��ֱ�������Σ���EDF��90�㣩����t��12ʱ����DEF��ֱ�������Σ���DEF��90�㣩��
ʱ��DEF��ֱ�������Σ���EDF��90�㣩����t��12ʱ����DEF��ֱ�������Σ���DEF��90�㣩��


 ����ѧҵ���Ե�����ϵ�д�
����ѧҵ���Ե�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD�У�E��F�ֱ���AD��BC�ߵ��е㣬G��H�ǶԽ���BD�ϵ����㣬��BG��DH�������н����в���ȷ���ǣ�������
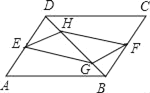
A. GF��FHB. GF��EH
C. EF��AC����ƽ��D. EG��FH
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
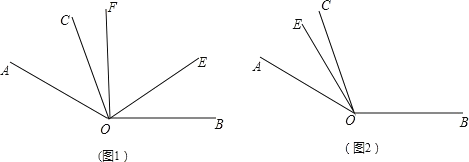
����Ŀ����ͼ1,��֪��AOB=![]() ,��AOC=
,��AOC=![]() ��OE�ǡ�AOB�ڲ���һ�����ߣ���OFƽ�֡�AOE.
��OE�ǡ�AOB�ڲ���һ�����ߣ���OFƽ�֡�AOE.
(1)����EOB=![]() �����COF�Ķ�����
�����COF�Ķ�����
(2)����COF=![]() �����EOB�Ķ���(�ú�n��ʽ�ӱ�ʾ����
�����EOB�Ķ���(�ú�n��ʽ�ӱ�ʾ����
(3)������OE�Ƶ�O��ʱ����ת����ͼ2��λ��ʱ�����ͼ������������ʱ����COF���EOB��������������ϵ?��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������![]() �뷴��������
�뷴��������![]() .
.
��1��֤����ֱ����˫����û�н��㣻
��2������ֱ��![]() ����ƽ��4����λ����˫����ǡ������ֻ��һ�����㣬���������ı���ʽ��ƽ�ƺ��ֱ�߱���ʽ��
����ƽ��4����λ����˫����ǡ������ֻ��һ�����㣬���������ı���ʽ��ƽ�ƺ��ֱ�߱���ʽ��
��3������2��С��ƽ�ƺ��ֱ�ߴ����ĺ�����Ϊ![]() ������ͼ��ֱ��д�������ڸ�ʵ��
������ͼ��ֱ��д�������ڸ�ʵ��![]() ����
����![]() ȡ��ֵʱ
ȡ��ֵʱ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ű߳�������ͬ��������ֽƬ����ͼ��ʽ�������ABCD�ڣ�����ֽƬ֮�以���ص�Ҳ��϶����δ������������ֽƬ���ǵIJ�������Ӱ��ʾ�������Ͻ������½���Ӱ���ֵ��ܳ��IJ�Ϊl����֪��l��ֵ������Ҫ��������֪���ܳ��������εı��Ϊ�� ��

A.��B.��C.��D.��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺���10b��n����ô��bΪn����������Ϊb��d��n����
��1�����������Ķ��壬��֪��d��10����1��d��102����2,��ô��d��103������ ����
��2�������������������ʣ���m��nΪ��������d��mn����d��m��+d��n���� d��![]() ����d��m����d��n������d��3����0.48��d��2����0.3�������������ʣ���գ�d��6������ ������d��
����d��m����d��n������d��3����0.48��d��2����0.3�������������ʣ���գ�d��6������ ������d��![]() ������ ����d��
������ ����d��![]() ������ ����
������ ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������״��С��ȫ��ͬ��С�����ο�Ƭ����ͼ�������ص��ķ���һ������Ϊ�����Σ���Ϊa���ף���Ϊb���ף��ĺ��ӵײ�����ͼ���������ӵ���δ����Ƭ���ǵIJ�������Ӱ��ʾ����ͼ����������Ӱ���ֵ��ܳ����ǣ� ��

A. 4a����B. 4b����C. 2��a+b������D. 4��a-b������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������1��2018��һ�������������±���
ƽ�Ʊ��д���Ӱ�ķ��������������ĺͿ����ǣ�������
A. 2018 B. 2019 C. 2040 D. 2049
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����һ����Ȼ�����Ա�ʾΪ�������������ĺͣ���ô���Ǿͳ������Ϊ�������������磺9=1+3+5������9������������.
��1������21��35�Dz�����������������˵�����ɣ�
��2���涨��![]()
![]() ������
������![]() ����
����![]() Ϊ��Ȼ�������Ƿ����һ������������
Ϊ��Ȼ�������Ƿ����һ������������![]() ��ʹ��
��ʹ��![]() 50=��3666.�����ڣ������
50=��3666.�����ڣ������![]() ������
������![]() ��ʾ��3�������������͵���ʽ���������ڣ���˵������.
��ʾ��3�������������͵���ʽ���������ڣ���˵������.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com