Question

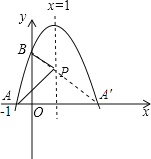
【题目】已知抛物线y=ax2+bx+4在坐标系中的位置如图所示，它与x，y轴的交点分别为A（﹣1，0），B，P是其对称轴x=1上的动点，根据图中提供的信息，得出以下结论：

①2a+b=0，

②x=3是方程ax2+bx+4=0的一个根，

③△PAB周长的最小值是5+，

④9a+4＜3b．

其中正确的是（ ）

A．1个 B．2个 C．3个 D．4个

Answer 1

【答案】D

【解析】

试题分析：①根据对称轴方程求得a、b的数量关系；

②根据抛物线的对称性知抛物线与x轴的另一个交点的横坐标是3；

③利用两点间直线最短来求△PAB周长的最小值；

④根据图象知，当x=﹣3时，y＜0，得到9a﹣3b+4＜0，即9a+4＜3b．

解：①根据图象知，对称轴是直线x=﹣=1，则b=﹣2a，即2a+b=0．

故①正确；

②根据图象知，点A的坐标是（﹣1，0），对称轴是x=1，则根据抛物线关于对称轴对称的性质知，抛物线与x轴的另一个交点的坐标是（3，0），所以x=3是ax2+bx+3=0的一个根，故②正确；

③如图所示，点A关于x=1对称的点是A′，即抛物线与x轴的另一个交点．

连接BA′与直线x=1的交点即为点P，

则△PAB周长的最小值是（BA′+AB）的长度．

∵A（﹣1，0），B（0，4），A′（3，0），

∴AB=，BA′=5．即△PAB周长的最小值是5+．

故③正确；

④根据图象知，当x=﹣3时，y＜0，

∴9a﹣3b+4＜0，即9a+4＜3b，

故④正确．

综上所述，正确的结论是：①②③④．

故选D．