

分析 (1)由题意得:这次调查中,一共调查的学生数为:40÷20%=200(名);
(2)根据题意可求得B占的百分比为:1-20%-30%-15%=35%,C的人数为:200×30%=60(名);则可补全统计图;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与一人是喜欢跳绳、一人是喜欢足球的学生的情况,再利用概率公式即可求得答案.
解答 解:(1)根据题意得:这次调查中,一共调查的学生数为:40÷20%=200(名);
故答案为:200;
(2)B占的百分比为:1-20%-30%-15%=35%,
C的人数为:200×30%=60(名);
如图:
(3)分别用A,B,C表示3名喜欢跳绳的学生,D表示1名喜欢足球的学生;
画树状图得:
∵共有12种等可能的结果,一人是喜欢跳绳、一人是喜欢足球的学生的有6种情况,
∴一人是喜欢跳绳、一人是喜欢足球的学生的概率为:$\frac{6}{12}$=$\frac{1}{2}$.
点评 此题考查了列表法或树状图法求概率以及条形统计图与扇形统计图.用到的知识点为:概率=所求情况数与总情况数之比.


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
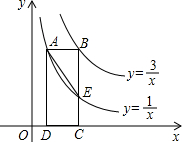 如图,矩形ABCD的一边CD在x轴上,顶点A、B分别落在双曲线y=$\frac{1}{x}$(x>0)、y=$\frac{3}{x}$(x>0)上,边BC交双曲线y=$\frac{1}{x}$(x>0)于点E,连接AE,则△ABE的面积为$\frac{2}{3}$.
如图,矩形ABCD的一边CD在x轴上,顶点A、B分别落在双曲线y=$\frac{1}{x}$(x>0)、y=$\frac{3}{x}$(x>0)上,边BC交双曲线y=$\frac{1}{x}$(x>0)于点E,连接AE,则△ABE的面积为$\frac{2}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
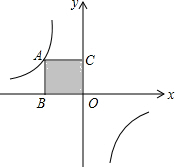 如图,点A是反比例函数y=$\frac{k}{x}$图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足点分别为B、C,矩形ABOC的面积为4,则k=-4.
如图,点A是反比例函数y=$\frac{k}{x}$图象上的一个动点,过点A作AB⊥x轴,AC⊥y轴,垂足点分别为B、C,矩形ABOC的面积为4,则k=-4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
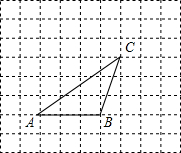 在正方形网格中,△ABC的位置如图所示,则sin∠BAC的值为( )
在正方形网格中,△ABC的位置如图所示,则sin∠BAC的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
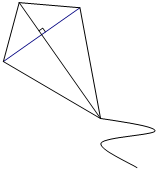 如图,小明将一根长为1.4米的竹条截为两段,并互相垂直固定,作为风筝的龙骨,制作成了一个面积为0.24米2的风筝.请你计算一下将竹条截成长度分别为多少的两段?
如图,小明将一根长为1.4米的竹条截为两段,并互相垂直固定,作为风筝的龙骨,制作成了一个面积为0.24米2的风筝.请你计算一下将竹条截成长度分别为多少的两段?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
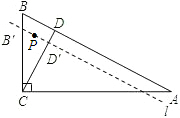 如图,在Rt△ABC中,∠ACB=90°,AC=$6\sqrt{3}$cm,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=$6\sqrt{3}$cm,BC=6cm,经过A,B的直线l以1cm/秒的速度向下作匀速平移运动,交BC于点B′,交CD于点 D′,与此同时,点P从点B′出发,在直线l上以1cm/秒的速度沿直线l向右下方向作匀速运动.设它们运动的时间为t秒.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com