
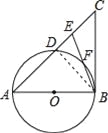
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.

【答案】(1)证明过程见解析;(2)1.6
【解析】试题分析:(1)由AE=AB,可得∠ABE=90°﹣![]() ∠BAC,又由∠BAC=2∠CBE,可求得∠ABC=∠ABE+∠CBE=90°,继而证得结论;
∠BAC,又由∠BAC=2∠CBE,可求得∠ABC=∠ABE+∠CBE=90°,继而证得结论;
(2)首先连接BD,易证得△ABD∽△ACB,然后由相似三角形的对应边成比例,求得答案.
试题解析:(1)∵AE=AB,
∴△ABE是等腰三角形,
∴∠ABE=![]() (180°﹣∠BAC=)=90°﹣
(180°﹣∠BAC=)=90°﹣![]() ∠BAC,
∠BAC,
∵∠BAC=2∠CBE,
∴∠CBE=![]() ∠BAC,
∠BAC,
∴∠ABC=∠ABE+∠CBE=(90°﹣![]() ∠BAC)+
∠BAC)+![]() ∠BAC=90°,
∠BAC=90°,
即AB⊥BC,
∴BC是⊙O的切线;
(2)连接BD,
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABC=90°,
∴∠ADB=∠ABC,
∵∠A=∠A,
∴△ABD∽△ACB,
∴![]() ,
,
∵在Rt△ABC中,AB=8,BC=6,
∴AC=![]() =10,
=10,
∴![]() ,
,
解得:AD=6.4,
∵AE=AB=8,
∴DE=AE﹣AD=8﹣6.4=1.6.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足当m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
是闭区间[1,2019]上的“闭函数”吗?请判断并说明理由.
(2)若一次函数y=kx+b(k≠0)是闭间[m,n]上的“闭函数”,求此函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
x2+bx+c的图象与坐标轴交于A,B,C三点,其中点A的坐标为(﹣3,0),点B的坐标为(4,0),连接AC,BC.动点P从点A出发,在线段AC上以每秒1个单位长度的速度向点C作匀速运动;同时,动点Q从点O出发,在线段OB上以每秒1个单位长度的速度向点B作匀速运动,当其中一点到达终点时,另一点随之停止运动,设运动时间为t秒.连接PQ.
(1)填空:b= ,c= ;
(2)在点P,Q运动过程中,△APQ可能是直角三角形吗?请说明理由;
(3)在x轴下方,该二次函数的图象上是否存在点M,使△PQM是以点P为直角顶点的等腰直角三角形?若存在,请求出运动时间t;若不存在,请说明理由;
(4)如图②,点N的坐标为(﹣![]() ,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.
,0),线段PQ的中点为H,连接NH,当点Q关于直线NH的对称点Q′恰好落在线段BC上时,请直接写出点Q′的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
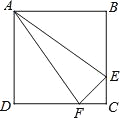
【题目】如图,正方形ABCD中,AB=4cm,点E、F同时从C点出发,以1cm/s的速度分别沿CB﹣BA、CD﹣DA运动,到点A时停止运动.设运动时间为t(s),△AEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
A. 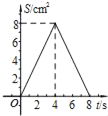 B.
B. 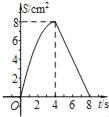
C. 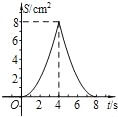 D.
D. 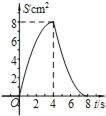
查看答案和解析>>
科目:初中数学 来源: 题型:
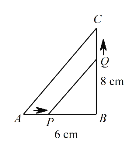
【题目】如图,在△ABC中,∠B=90°,AB=6厘米,BC=8厘米.点P从A点开始沿AB边向点B以1厘米/秒的速度移动(到达点B即停止运动),点Q从B点开始沿BC边向点C以2厘米/秒的速度移动(到达点C即停止运动).
(1)如果P,Q分别从A,B两点同时出发,经过几秒钟,△PBQ的面积等于△ABC面积的三分之一?
(2)如果P,Q两点分别从A,B两点同时出发,几秒钟后,P,Q相距6厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】晓东在解一元二次方程时,发现有这样一种解法:如:解方程x(x+4)=6.
解:原方程可变形,得[(x+2)﹣2][(x+2)+2]=6.(x+2)2﹣22=6,(x+2)2=6+22,(x+2)2=10.直接开平方并整理,得![]() ,
,![]() .我们称晓东这种解法为“平均数法”.
.我们称晓东这种解法为“平均数法”.
(1)下面是晓东用“平均数法”解方程(x+2)(x+6)=5时写的解题过程.
解:原方程可变形,得
[(x+□)﹣〇][(x+□)+〇]=5.
(x+□)2﹣〇2=5,
(x+□)2=5+〇2.
直接开平方并整理,得x1=☆,x2=¤.
上述过程中的“□”,“〇”,“☆”,“¤”表示的数分别为 , , , .
(2)请用“平均数法”解方程:(x﹣3)(x+1)=5.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学习了三角形全等的判定方法(即SSS,SAS,ASA,AAS)和直角三角形全等的判定方法(即HL)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
(初步思考)
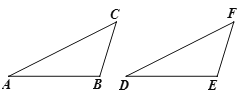
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后对∠B进行分类,可以分为“∠B是直角、钝角、锐角”三种情况进行探究.
(深入探究)
第一种情况:当∠B为锐角时,△ABC和△DEF不一定全等.
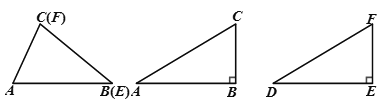
(1)如图,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角,请你用尺规在图中确定点D,使△DEF和△ABC不全等(不写作法,保留作图痕迹);
第二种情况:当∠B为直角时,△ABC≌△DEF.
(2)如图,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据____,可以知道Rt△ABC≌Rt△DEF.
第三种情况:当∠B为钝角时,△ABC≌△DEF.
(3)如图,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是钝角,求证:△ABC≌△DEF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com