
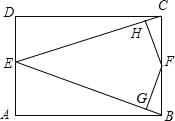
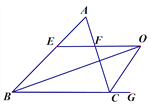
【题目】如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( ).
A.![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
![]()
【答案】D.
【解析】
试题分析:先连接EF,由矩形的性质得出AB=CD=3,AD=BC=2,∠A=∠D=90°,由勾股定理求出BE,由SAS证明△ABE≌△DCE,得出BE=CE=![]() ,再由△BCE的面积=△BEF的面积+△CEF的面积,即可得出结果.如图所示:∵四边形ABCD是矩形,∴AB=CD=3,AD=BC=2,∠A=∠D=90°,∵点E为AD中点,∴AE=DE=1,∴BE=
,再由△BCE的面积=△BEF的面积+△CEF的面积,即可得出结果.如图所示:∵四边形ABCD是矩形,∴AB=CD=3,AD=BC=2,∠A=∠D=90°,∵点E为AD中点,∴AE=DE=1,∴BE=![]() =
=![]() =
=![]() ,在△ABE和△DCE中,
,在△ABE和△DCE中,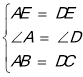 ,∴△ABE≌△DCE(SAS),∴BE=CE=
,∴△ABE≌△DCE(SAS),∴BE=CE=![]() ,∵△BCE的面积=△BEF的面积+△CEF的面积,∴
,∵△BCE的面积=△BEF的面积+△CEF的面积,∴![]() BC×AB=
BC×AB=![]() BE×FG+
BE×FG+![]() CE×FH,即BE(FG+FH)=BC×AB,即
CE×FH,即BE(FG+FH)=BC×AB,即![]() (FG+FH)=2×3,解得:FG+FH=
(FG+FH)=2×3,解得:FG+FH=![]() ;故选:D.
;故选:D.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】已知如图:△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC交AB、AC于E、F.
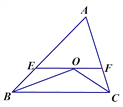
(1)图中有几个等腰三角形?试说明理由,并请指出EF与BE、CF间有怎样的关系?
(2)若△ABC中,∠B的平分线与三角形外角∠ACG的平分线CO交于点O,过O点作OE∥BC交AB于E,交AC于F(如图2),请直接写出EF与BE、CF间的关系,不用证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=12,点C、D在AB上,且AC=DB=2,点P从点C沿线段CD向点D运动(运动到点D停止),以AP、BP为斜边在AB的同侧画等腰Rt△APE和等腰Rt△PBF,连接EF,取EF的中点G,下列说法中正确的有( )

①△EFP的外接圆的圆心为点G;②四边形AEFB的面积不变;③EF的中点G移动的路径长为4.
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE= 度;
(2)设∠BAC=α,∠BCE=β.
①如图2,当点D在线段BC上移动,则α,β之间有怎样的数量关系?请说明理由;
②当点D在直线BC上移动,则α,β之间有怎样的数量关系?请直接写出你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售出2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各为多少元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元.则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售A,B两种型号计算器,A型号计算器的进货价格为每台30元,B型号计算器的进货价格为每台40元.商场销售5台A型号和1台B型号计算器,可获利润76元;销售6台A型号和3台B型号计算器,可获利润120元.
(1)分别求商场销售A,B两种型号计算器每台的销售价格.
(2)商场准备用不多于2 500元的资金购进A、B两种型号计算器共70台,问最少需要购进A型号的计算器多少台?【利润=销售价格﹣进货价格】
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com