
如图,在Rt△ABC中,∠C = 90°,∠BAC的平分线AD交BC边于点D.以AB上一点O为圆心作⊙O,使⊙O经过点A和点D.
(1)判断直线BC与⊙O的位置关系,并说明理由;
(2)若AC = 3,∠B = 30°.
①求⊙O的半径;
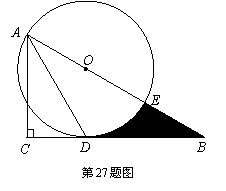 ②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的面积.(结果保留根号和
②设⊙O与AB边的另一个交点为E,求线段BD、BE与劣弧DE所围成的阴影部分的面积.(结果保留根号和 )
)
解:(1)直线BC与⊙O相切;……………………1分
连结OD,………………………………………2分
∵OA = OD ∴∠OAD = ∠ODA
∵∠BAC的角平分线AD交BC边于D
∴∠CAD = ∠OAD
∴∠CAD = ∠ODA
∴OD∥AC ……………………………………3分
∴∠ODB = ∠C = 90°
即OD⊥BC. ………………………………………………………………………………4分
∴直线BC与⊙O相切.
(2)①设OA = OD = r,在Rt△B DO中,∠B = 30°,
DO中,∠B = 30°,
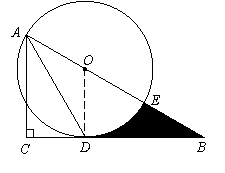 ∴OB = 2r ………………………………………
∴OB = 2r ……………………………………… …
… ……………………………………5分
……………………………………5分
在Rt△ACB中,∠B = 30°
∴AB = 2AC = 6
∴3r = 6 …………………………………………………………………………………6分
解得r = 2. ……………………………………………………………………7分
②在Rt△ACB中,∠B = 30°,
∴∠BOD = 60°. …………………………………………………………………………8分∴S扇形ODE=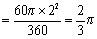 . ……………………………………………………………9分
. ……………………………………………………………9分
∴所求图形面积为:S△BOD- S扇形ODE 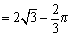 .……………………………………10分
.……………………………………10分


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
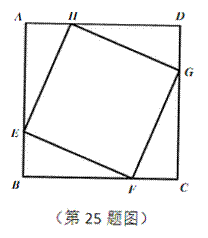 如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA 上的动点,且AE=BF=CG=DH.
如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA 上的动点,且AE=BF=CG=DH.
(1)求证:四边形EFGH是正方形;
(2)判断直线EG是否经过一个定点,并说明理由;
(3)求四边形EFGH面积的最小值。
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
如图,在图中求作⊙P,使⊙P满足以线段MN为弦且圆心P到∠AOB两边的距离相等.(要求:尺规作图,不写作法,保留作图痕迹,并把作图痕迹用黑色签字笔加黑)
查看答案和解析>>
科目:初中数学 来源: 题型:
某校要从四名学生中选拔一名参加市“风华小主播”大赛,选拔赛中每名学生的平均成绩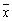 及其方差
及其方差 如表所示.如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是
如表所示.如果要选择一名成绩高且发挥稳定的学生参赛,则应选择的学生是
A.甲 B.乙
 C.丙 D.丁
C.丙 D.丁
| 甲 | 乙 | 丙 | 丁 | |
| 8 | 9 | 9 | 8 | |
|
| 1 | 1 | 1.2 | 1.3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,△ABC的三个顶点和它内部的点P1,把△ABC分成3个互不重叠的小三角形;△ABC的三个顶点和它内部的点P1、P2,把△ABC分 成5个互不重叠的小三角形;△ABC的三个顶点和它内部的点 P1、P2、P3,把△ABC分成7个互不重叠的小三角形;…△ABC的三个顶点和它内部的点 P1、P2、P3、…、Pn,把△ABC分成 个互不重叠的小三角形.
成5个互不重叠的小三角形;△ABC的三个顶点和它内部的点 P1、P2、P3,把△ABC分成7个互不重叠的小三角形;…△ABC的三个顶点和它内部的点 P1、P2、P3、…、Pn,把△ABC分成 个互不重叠的小三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com