
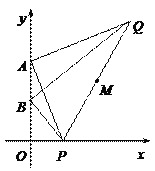
【题目】如图,A、B两点的坐标分别为(0,4),(0,2),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.
(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;
(2)当⊙M与x轴相切时,求点Q的坐标;
(3)当点P从点(1,0)运动到点(2,0)时,请直接写出线段QM扫过图形的面积.


【答案】(1)见解析;(2)(2![]() ,6);(3)
,6);(3)![]() .
.
【解析】试题分析:(1)连接AM、BM,由△APQ和△BPQ都是直角三角形,M是斜边PQ的中点,可得AM=BM=PM=QM,从而问题得证;
(2) 作MG⊥y轴于G,MC⊥x轴于C,由已知求得MC=OG=3,确定出在点P运动的过程中,点M到x轴的距离始终为3,从而确定点Q的纵坐标始终为6, 当⊙M与x轴相切时则PQ⊥x轴,作QH⊥y轴于H,由△BOP∽△QHB,根据相似三角形的性质即可得;
(3)由相似可得:当点P在P1(1,0)时,Q1(8,6)则M1(![]() ,3),当点P在P2(2,0)时,Q2(4,6),则M2(3,3),根据线段QM扫过的图形为梯形M1M2Q2Q1,根据梯形的面积公式进行计算即可得.
,3),当点P在P2(2,0)时,Q2(4,6),则M2(3,3),根据线段QM扫过的图形为梯形M1M2Q2Q1,根据梯形的面积公式进行计算即可得.
试题解析:(1)连接AM、BM,
∵△APQ和△BPQ都是直角三角形,M是斜边PQ的中点,
∴AM=BM=PM=QM=![]() PQ,
PQ,
∴A、B、P、Q四点在以M为圆心的同一个圆上;
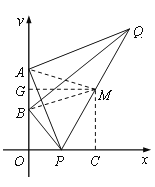
(2) 作MG⊥y轴于G,MC⊥x轴于C,∵AM=BM,
∴G是AB的中点,由A(0,4),B(0,2)可得MC=OG=3,
∴在点P运动的过程中,点M到x轴的距离始终为3,
则点Q到x轴的距离始终为6,即点Q的纵坐标始终为6,
当⊙M与x轴相切时则PQ⊥x轴,作QH⊥y轴于H,
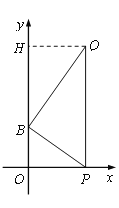
HB=6-2=4,设OP=HQ=x,
由△BOP∽△QHB,得x 2=2×4=8,x=2![]() ,
,
∴点Q的坐标为(2![]() ,6);
,6);
(3)由相似可得:当点P在P1(1,0)时,Q1(8,6),则M1(![]() ,3),
,3),
当点P在P2(2,0)时,Q2(4,6),则M2(3,3),
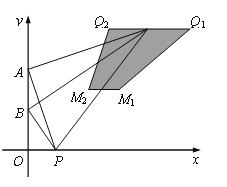
∴M1M2= ![]() -3=
-3=![]() ,Q1Q2=8-4=4,
,Q1Q2=8-4=4,
线段QM扫过的图形为梯形M1M2Q2Q1,
其面积为: ![]() ×(
×(![]() +4 )×3=
+4 )×3=![]() .
.


科目:初中数学 来源: 题型:
【题目】某饮品店老板新推出A、B两种囗味的饮料,其中每杯A种口味饮料的利润率为60%,每杯B种口味饮料的利润率为20%.当售出的A种口味的杯数比B种口味的杯数少50%时,这个老板得到的总利润率为36%;当售出的A种口味的杯数比B种口味的杯数多25%时,这个老板得到的总利润率为_____.(利润率=利润÷成本)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于点A(1,6),B(3,n)两点.
的图象交于点A(1,6),B(3,n)两点.
(1)求一次函数的表达式;
(2)在y轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
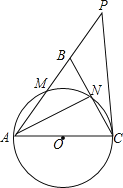
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O分别交AB、BC于点M、N,直线CP是⊙O的切线,且点P在AB的延长线上.
(1)若∠P=40°,求∠BCP的度数;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求点B到AC的距离.
,求点B到AC的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买![]() 两种型号的垃圾处理设备共10台,已知每台
两种型号的垃圾处理设备共10台,已知每台![]() 型设备日处理能力为12吨;每台
型设备日处理能力为12吨;每台![]() 型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买![]() 两种设备的方案;
两种设备的方案;
(2)已知每台![]() 型设备价格为3万元,每台
型设备价格为3万元,每台![]() 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )

A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;并用含α的式子表示∠AMB的度数;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com