
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O分别交AB、BC于点M、N,直线CP是⊙O的切线,且点P在AB的延长线上.
(1)若∠P=40°,求∠BCP的度数;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求点B到AC的距离.
,求点B到AC的距离.
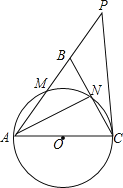
【答案】(1)25°;(2)4
【解析】试题分析:(1)根据CP是⊙O的切线,AC为直径,可得∠ACP=90°,再由∠P=40°从而可得∠BAC=50°,再根据AB=AC求得∠ABC的度数即可得;
(2)作BF⊥AC于F,由题意可得∠ANC=90°,再根据等腰三角形的性质求得CN长,再根据直角三角形两锐角互余推得∠BCP=∠CAN,由已知即可得sin∠CAN=![]() ,从而可得.
,从而可得.
试题解析:(1)∵CP是⊙O的切线,AC为直径,
∴∠ACP=90°,
又∵∠P=40°,
∴∠BAC=50°,
∵AB=AC,
∴∠ABC=∠ACB=65°,
∴∠BCP =∠ABC-∠P=65°-40°=25°;
(2)如图,作BF⊥AC于F,
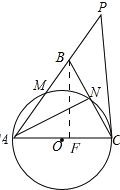
∵AC为直径,
∴∠ANC=90°,
∵AB=AC,
∴CN=![]() CB=
CB=![]() ,
,
∵∠BCP+∠ACN =∠CAN+∠ACN,
∴∠BCP=∠CAN,
∵sin∠BCP=![]() ,
,
∴sin∠CAN=![]() ,
,
∴![]() ,
,
∴AC=5,


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=a(x+![]() )2+k(a>0),点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)是图象上的三个点,则y1、y2、y3的大小关系是_____(用“<”连接).
)2+k(a>0),点A(﹣4,y1)、B(﹣2,y2)、C(2,y3)是图象上的三个点,则y1、y2、y3的大小关系是_____(用“<”连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
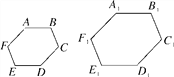
【题目】图中的两个多边形ABCDEF和A1B1C1D1E1F1相似(各字母已按对应关系排列),∠A=∠D1=135°,∠B=∠E1=120°,∠C1=95°.
(1)求∠F的度数;
(2)如果多边形ABCDEF和A1B1C1D1E1F1的相似比是1:1.5,且CD=15cm,求C1D1的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中∠ABC=90°,,AB=4 cm, BC=3cm,动点P以3cm/s的速度由A向C运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交AB于D,则当运动时间为____s时,△ADP是以AP为腰的等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在第1个![]() 中,
中,![]() ;在边
;在边![]() 上任取一点
上任取一点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,得到第2个
,得到第2个![]() ;在边
;在边![]() 上任取一点
上任取一点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,得到第3个
,得到第3个![]() …按此做法继续下去,则第
…按此做法继续下去,则第![]() 个三角形中以
个三角形中以![]() 为顶点的底角度数是( )
为顶点的底角度数是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
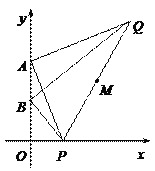
【题目】如图,A、B两点的坐标分别为(0,4),(0,2),点P为x轴正半轴上一动点,过点A作AP的垂线,过点B作BP的垂线,两垂线交于点Q,连接PQ,M为线段PQ的中点.
(1)求证:A、B、P、Q四点在以M为圆心的同一个圆上;
(2)当⊙M与x轴相切时,求点Q的坐标;
(3)当点P从点(1,0)运动到点(2,0)时,请直接写出线段QM扫过图形的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
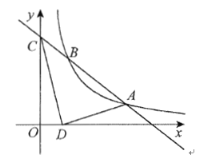
【题目】如图,已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)反比例函数的表达式 ;一次函数的表达式 .
(2)若在![]() 轴上有一点
轴上有一点![]() ,其横坐标是1,连接
,其横坐标是1,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG,当点E在线段BC上时,如图1,易证:AB=CG+CE.
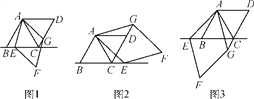
(1)当点E在线段BC的延长线上时(如图2),猜想AB,CG,CE之间的关系并证明;
(2)当点E在线段CB的延长线上时(如图3),直接写出AB,CG,CE之间的关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com