
【题目】已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG,当点E在线段BC上时,如图1,易证:AB=CG+CE.
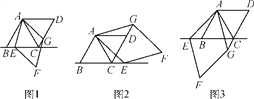
(1)当点E在线段BC的延长线上时(如图2),猜想AB,CG,CE之间的关系并证明;
(2)当点E在线段CB的延长线上时(如图3),直接写出AB,CG,CE之间的关系.
【答案】(1)AB=CG-CE(2)AB=CE-CG
【解析】试题分析:(1)根据菱形的性质可得AC=AD,AE=AG,然后证明∠DAG=∠CAE,可利用SAS证明△ACE≌△ADG,根据全等三角形的性质可得CE=DG,再根据线段的和差关系和等量代换可得答案;
(2)方法与(1)类似可证明△ACG≌△ABE,进而得到BE=CG,然后可得AB=CE﹣CG.
试题解析:(1)AB=CG-CE
∵AC是菱形ABCD的对角线且∠BAC=60°,∴AC=AD.
∵四边形AEFG菱形,∴AE=AG..
∵∠DAC=∠GAE ="60°," ∴∠DAG=∠CAE.
∴△ACE≌△ADG(SAS), ∴CE=DG..
∴AB=CD=CG-DG=CG-CE
(2). AB =" CE-" CG.
同理可证△ACG ≌△ABE(SAS),∴BE=CG..
∴AB ="CB=" CE- BE=CE-CG.


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】如图在Rt△ABC中,∠C=90°,点D是AC的中点,且∠A+∠CDB=90°,过点A、D作⊙O,使圆心O在AB上,⊙O与AB交于点E.
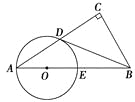
(1)求证:直线BD与⊙O相切;
(2)若AD:AE=4:5,BC=6,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O分别交AB、BC于点M、N,直线CP是⊙O的切线,且点P在AB的延长线上.
(1)若∠P=40°,求∠BCP的度数;
(2)若BC=2![]() ,sin∠BCP=
,sin∠BCP=![]() ,求点B到AC的距离.
,求点B到AC的距离.
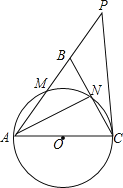
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买![]() 两种型号的垃圾处理设备共10台,已知每台
两种型号的垃圾处理设备共10台,已知每台![]() 型设备日处理能力为12吨;每台
型设备日处理能力为12吨;每台![]() 型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买![]() 两种设备的方案;
两种设备的方案;
(2)已知每台![]() 型设备价格为3万元,每台
型设备价格为3万元,每台![]() 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的黑色圆点按照一定规律所组成的,其中第①个图形中一共有6个黑色圆点第②个图形中一共有15个黑色圆点,第③个图形中一共有28个黑色圆点,…,按此规律排列下去,第⑦个图形中黑色圆点的个数为( )

A.66B.91C.120D.135
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD,AE于H,G,则BH:HG:GM等于( )

A. 4:2:1 B. 5:3:1 C. 25:12:5 D. 51:24:10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.
(1)如图①,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
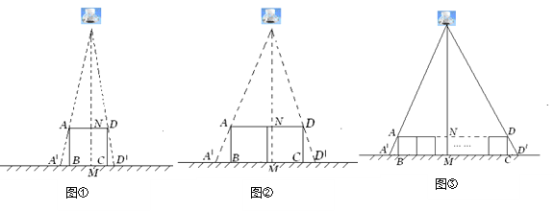 (2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(2)不改变①中灯泡的高度,将两个边长为30cm的正方形框架按图②摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图③摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是 .
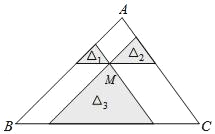
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形![]() 中,
中,![]() .
.

(1)如图1,点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 的延长线上取一点
的延长线上取一点![]() ,使得
,使得![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .判断
.判断![]() 与
与![]() 有怎样的数量关系,写出你的结论,并加以证明;
有怎样的数量关系,写出你的结论,并加以证明;
(2)如图2,点![]() 在线段
在线段![]() 的延长线上,在线段
的延长线上,在线段![]() 的延长线上取一点
的延长线上取一点![]() ,使得
,使得![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.
①依题意补全图形;
②若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com