
【题目】如图,在直角三角形![]() 中,
中,![]() .
.

(1)如图1,点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 的延长线上取一点
的延长线上取一点![]() ,使得
,使得![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .判断
.判断![]() 与
与![]() 有怎样的数量关系,写出你的结论,并加以证明;
有怎样的数量关系,写出你的结论,并加以证明;
(2)如图2,点![]() 在线段
在线段![]() 的延长线上,在线段
的延长线上,在线段![]() 的延长线上取一点
的延长线上取一点![]() ,使得
,使得![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.
①依题意补全图形;
②若![]() ,求证:
,求证:![]() .
.
【答案】(1)∠ENB=∠NAC,理由见解析;(2)①见解析;②见解析;
【解析】
(1)依据∠NFD=∠ADB=90°,∠ACB=90°,即可得到∠FAC+∠AMC=∠FNC+∠AMC=90°,进而得出∠MAC=∠ENB,再根据∠NAC=∠MAC,即可得到∠ENB=∠NAC;
(2)①过点B作BD⊥AM于点D,过点N作NE∥BD,交BA延长线于点E,交MA延长线于点F;②依据∠ENB=∠NAC,∠NEA=135°-∠ENB,∠EAN=135°-∠NAC,即可得到∠NEA=∠NAE.
(1)∠ENB与∠NAC之间的数量关系:∠ENB=∠NAC,
理由:∵BD⊥AM,
∴∠ADB=90°,
∵NE∥BD,
∴∠NFD=∠ADB=90°,
∵∠ACB=90°,
∴∠FAC+∠AMC=∠FNC+∠AMC=90°,
∴∠MAC=∠ENB,
又∵∠NAC=∠MAC,
∴∠ENB=∠NAC;
(2)①补全图形如图:
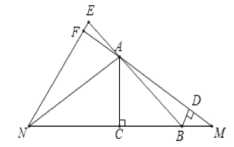
②同理可证∠ENB=∠NAC,
∵在Rt△ABC中,∠ACB=90°,∠CAB=45°,
∴∠ABC=45°,
∴∠ABM=135°,
∴∠NEA=∠ABM∠NEB=135°∠ENB,
∵∠EAN=∠EAB∠NAC∠CAB=135°∠NAC,
∴∠NEA=∠NAE.


科目:初中数学 来源: 题型:
【题目】已知AC是菱形ABCD的对角线,∠BAC=60°,点E是直线BC上的一个动点,连接AE,以AE为边作菱形AEFG,并且使∠EAG=60°,连接CG,当点E在线段BC上时,如图1,易证:AB=CG+CE.
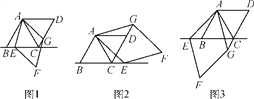
(1)当点E在线段BC的延长线上时(如图2),猜想AB,CG,CE之间的关系并证明;
(2)当点E在线段CB的延长线上时(如图3),直接写出AB,CG,CE之间的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在![]() 中,
中,![]() 是高,
是高,![]() 是角平分线,当
是角平分线,当![]() ,
,![]() ,则
,则![]() ____
____![]() ;
;

(2)若![]() 和
和![]() 的度数分别用字母
的度数分别用字母![]() 和
和![]() 来表示(
来表示(![]() ),你能找到
),你能找到![]() 与
与![]() 和
和![]() 之间的关系吗? ______.(请直接写出你发现的结论)
之间的关系吗? ______.(请直接写出你发现的结论)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知灯塔M方圆一定范围内有镭射辅助信号,一艘轮船在海上从南向北方向以一定的速度匀速航行,轮船在A处测得灯塔M在北偏东30°方向,行驶1小时后到达B处,此时刚好进入灯塔M的镭射信号区,测得灯塔M在北偏东45°方向,则轮船通过灯塔M的镭射信号区的时间为( )
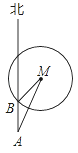
A. (![]() ﹣1)小时 B. (
﹣1)小时 B. (![]() +1)小时 C. 2小时 D.
+1)小时 C. 2小时 D. ![]() 小时
小时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少________个时,网球可以落入桶内.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)如图①所示,将直尺摆放在三角板ABC上,使直尺与三角板的边分别交于点D,E,F,G,量得∠CGD=42°。

(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B,交AC边于点H,如图②所示.点H,B在直尺上的读数分别为4,13.4,求BC的长(结果保留两位小数).
(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
科目:初中数学 来源: 题型:
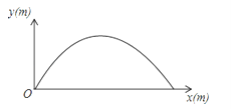
【题目】如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=﹣![]() x2+
x2+![]() x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.
x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.
(1)飞行的水平距离是多少时,球最高?
(2)球从飞出到落地的水平距离是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com