
【题目】(1)如图,在![]() 中,
中,![]() 是高,
是高,![]() 是角平分线,当
是角平分线,当![]() ,
,![]() ,则
,则![]() ____
____![]() ;
;

(2)若![]() 和
和![]() 的度数分别用字母
的度数分别用字母![]() 和
和![]() 来表示(
来表示(![]() ),你能找到
),你能找到![]() 与
与![]() 和
和![]() 之间的关系吗? ______.(请直接写出你发现的结论)
之间的关系吗? ______.(请直接写出你发现的结论)
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)依据三角形内角和定理即可得到∠BAC的度数,再根据角平分线进行计算,即可得到∠EAD的度数;
(2)直接运用(1)中的计算方法,即可得到∠EAD与α和β之间的关系.
(1)∵∠B=20°,∠C=60°,
∴在△ABC中,∠BAC=180°∠B∠C=100°,
依据AE是角平分线,得∠BAE=![]() ∠BAC=50°,
∠BAC=50°,
又∵AD⊥BC,
∴∠BAD=90°∠B=70°,
∴∠EAD=∠BAD∠BAE=70°50°=20°.
(2)∠EAD=![]() (βα),
(βα),
证明:在△ABC中,∠BAC=180°∠B∠C=180°αβ,
依据AE是角平分线,得∠BAE=![]() ∠BAC=90°
∠BAC=90°![]() (α+β),
(α+β),
又∵AD⊥BC,
∴∠BAD=90°∠B=90°α,
∴∠EAD=∠BAD∠BAE=90°α90°+![]() (α+β)=
(α+β)=![]() (βα).
(βα).


科目:初中数学 来源: 题型:
【题目】“绿水青山,就是金山银山”.某旅游景区为了保护环境,需购买![]() 两种型号的垃圾处理设备共10台,已知每台
两种型号的垃圾处理设备共10台,已知每台![]() 型设备日处理能力为12吨;每台
型设备日处理能力为12吨;每台![]() 型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
型设备日处理能力为15吨,购回的设备日处理能力不低于140吨.
(1)请你为该景区设计购买![]() 两种设备的方案;
两种设备的方案;
(2)已知每台![]() 型设备价格为3万元,每台
型设备价格为3万元,每台![]() 型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
型设备价格为4.4万元.厂家为了促销产品,规定货款不低于40万元时,则按9折优惠;问:采用(1)设计的哪种方案,使购买费用最少,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
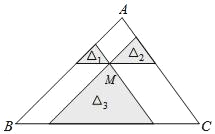
【题目】如图,点M是△ABC内一点,过点M分别作直线平行于△ABC的各边,所形成的三个小三角形△1、△2、△3(图中阴影部分)的面积分别是1、4、25.则△ABC的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,AC=BC,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点M,连接CM.
(1)求证:BE=AD;并用含α的式子表示∠AMB的度数;
(2)当α=90°时,取AD,BE的中点分别为点P、Q,连接CP,CQ,PQ,如图2,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,二次函数y1=(x﹣2)(x﹣4)的图象与x轴交于A、B两点(点A在点B的左侧),其对称轴l与x轴交于点C,它的顶点为点D.
(1)写出点D的坐标 .
(2)点P在对称轴l上,位于点C上方,且CP=2CD,以P为顶点的二次函数y2=ax2+bx+c(a≠0)的图象过点A.
①试说明二次函数y2=ax2+bx+c(a≠0)的图象过点B;
②点R在二次函数y1=(x﹣2)(x﹣4)的图象上,到x轴的距离为d,当点R的坐标为 时,二次函数y2=ax2+bx+c(a≠0)的图象上有且只有三个点到x轴的距离等于2d;
③如图2,已知0<m<2,过点M(0,m)作x轴的平行线,分别交二次函数y1=(x﹣2)(x﹣4)y2=ax2+bx+c(a≠0)的图象于点E、F、G、H(点E、G在对称轴l左侧),过点H作x轴的垂线,垂足为点N,交二次函数y1=(x﹣2)(x﹣4)的图象于点Q,若△GHN∽△EHQ,求实数m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级261位学生参加期末考试,某班35位学生的语文成绩、数学成绩与总成绩在全年级中排名情况如图1和图2所示,甲、乙、丙为该班三位学生.

从这次考试成绩看,①在甲、乙两人中,总成绩名次靠前的学生是______;
②在语文和数学两个科目中,丙同学的成绩名次更靠前的科目是______.
你选择的理由是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形![]() 中,
中,![]() .
.

(1)如图1,点![]() 在线段
在线段![]() 上,在线段
上,在线段![]() 的延长线上取一点
的延长线上取一点![]() ,使得
,使得![]() .过点
.过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .判断
.判断![]() 与
与![]() 有怎样的数量关系,写出你的结论,并加以证明;
有怎样的数量关系,写出你的结论,并加以证明;
(2)如图2,点![]() 在线段
在线段![]() 的延长线上,在线段
的延长线上,在线段![]() 的延长线上取一点
的延长线上取一点![]() ,使得
,使得![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,交
,交![]() 延长线于点
延长线于点![]() .
.
①依题意补全图形;
②若![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从谢家集到田家庵有3路,121路,26路三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从谢家集到田家庵的用时时间,在每条线路上随机选取了450个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
用时的频数 用时 线路 |
|
|
| 合计 |
3路 | 260 | 167 | 23 | 450 |
121路 | 160 | 166 | 124 | 450 |
26路 | 50 | 122 | 278 | 450 |
早高峰期间,乘坐__________(“3路”,“121路”或“26路”)线路上的公交车,从谢家集到田家庵“用时不超过50分钟”的可能性最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB的中点)所在的直线上,得到经过点D的折痕DE,若菱形边长为1,则点E到CD的距离为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com