练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

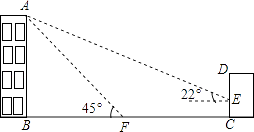
    【题目】如图，某教学楼AB的后面有一建筑物CD，当光线与地面夹角是22°时，教学楼在建筑物的墙上留下高2米的影子CE；而当光线与地面夹角是45°时，教学楼顶A在地面上的影子F与墙角C有13米的距离（B、F、C在一条直线上），求教学楼AB的高度（sin22°≈ ，cos22°≈ ，tan22°≈ ）

    【答案】解：（1）过点E作EM⊥AB，垂足为M．

    设AB为x．

    Rt△ABF中，∠AFB=45°，

    ∴BF=AB=x，

    ∴BC=BF+FC=x+13，

    在Rt△AEM中，∠AEM=22°，AM=AB﹣BM=AB﹣CE=x﹣2，

    tan22°= ，

    则 = ，

    解得：x=12．

    即教学楼的高12m．


    【解析】首先构造直角三角形△AEM，利用tan22°= ，求出即可；

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】四个全等的直角三角形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为的小正方形EFGH，已知AM为Rt△ABM较长直角边，AM=EF，则正方形ABCD的面积为（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一辆货车从仓库O出发在东西街道上运送水果，规定向东为正方向，一次到达的5个销售地点依次分别为A，B，C，D，E，最后回到仓库O，货车行驶的记录（单位：千米）如下：+1，+3，﹣6，﹣1，﹣2，+5．请问：

    （1）请以仓库O为原点，向东为正方向，选择适当的单位长度，画出数轴，并标出A，B，C，D，E的位置；

    （2）试求出该货车共行驶了多少千米？

    （3）如果货车运送的水果以100千克为标准重量，超过的千克数记为正数，不足的千克数记为负数，则运往A，B，C，D，E五个地点的水果重量可记为：

    +50，﹣15，+25，﹣10，﹣15，则该货车运送的水果总重量是多少千克？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A（3，﹣6）是二次函数y=ax2上的一点，则这二次函数的解析式是 ．

    【答案】y=﹣x2

    【解析】

    试题分析：将点A（3，﹣6）代入y=ax2，利用待定系数法法求该二次函数的解析式即可得﹣6=9a，

    解得a=﹣；因此该二次函数的解析式为：y=﹣x2．

    考点：待定系数法求二次函数解析式

    【题型】填空题
    【结束】
    15

    【题目】在一个不透明的口袋中装有8个红球和若干个白球，它们除颜色外其它完全相同，通过多次摸球试验后发现，摸到红球的频率稳定在40%附近，则口袋中白球可能有________个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】现有一块三角形的空地，其三边的长分别为20m，30m，40m，现要把它分成面积为2：3：4的三部分，分别种植不同的花草，请你设计一种方案，并简单说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，菱形ABCD的顶点C与原点O重合，点B在y轴的正半轴上，点A在反比例函数y= （k＞0，x＞0）的图象上，点D的坐标为（4，3）．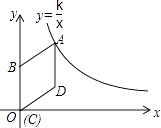

    （1）求k的值；
    （2）若将菱形ABCD沿x轴正方向平移，当菱形的顶点D落在函数y= （k＞0，x＞0）的图象上时，求菱形ABCD沿x轴正方向平移的距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，边长为2的正方形ABCD中，点P在AB边上（不与点A、B重合），点Q在BC边上（不与点B、C重合）
    第一次操作：将线段PQ绕点Q顺时针旋转，当点P落在正方形上时，记为点M；
    第二次操作：将线段QM绕点M顺时针旋转，当点Q落在正方形上时，记为点N；
    依次操作下去…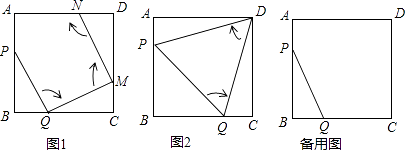

    （1）如图2，经过两次操作后得到△PQD、△PQD的形状是 ， 求此时线段PQ的长 ；
    （2）若经过三次操作可得到四边形PQMN．
    ①请直接判断四边形PQMN的形状，直接写出此时此刻AP与BQ的数量关系；
    ②以①中的结论为前提，直接写出四边形PQMN的面积的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

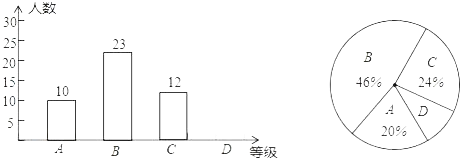
    【题目】某校为了解七年级学生体育测试情况，以七年级（1）班学生的体育测试成绩为样本，按A，B，C，D四个等级进行统计，并将统计结果绘制成如下的统计图，请你结合图中所给信息解答下列问题：

    （说明：A级：90分～100分；B级：75分～89分；C级：60分～74分；D级：60分以下）

    （1）计算D级的学生人数，并把条形统计图补充完整；

    （2）计算扇形统计图中A级所在的扇形的圆心角度数：

    （3）若该校七年级有600名学生，请估计体育测试中B级学生人数约为多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

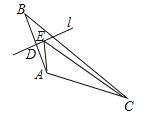
    【题目】如图，在△ABC中，点D是AB边的中点，过点D作边AB的垂线l，E是l上任意一点，且AC=5，BC=8，则△AEC的周长最小值为______．

    查看答案和解析>>

    同步练习册答案