
【题目】如图,∠ABC=90°,O为射线BC上一点,以点O为圆心, ![]() OB长为半径作⊙O,将射线BA绕点B按顺时针方向旋转至BA′,若BA′与⊙O相切,则旋转的角度α(0°<α<180°)等于 .
OB长为半径作⊙O,将射线BA绕点B按顺时针方向旋转至BA′,若BA′与⊙O相切,则旋转的角度α(0°<α<180°)等于 . 
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣4x+3.
(1)把这个二次函数化成y=a(x﹣h)2+k的形式;
(2)写出二次函数的对称轴和顶点坐标;
(3)求二次函数与x轴的交点坐标;
(4)画出这个二次函数的图象; 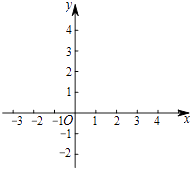
(5)观察图象并写出y随x增大而减小时自变量x的取值范围.
(6)观察图象并写出当x为何值时,y>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,AD=4,将矩形ABCD绕点D顺时针旋转90°得到矩形A′B′C′D′,则点B经过的路径与BA,AC′,C′B′所围成封闭图形的面积是多少?(结果保留π). 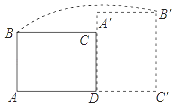
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为直线x=﹣1,与x轴的一个交点为(1,0),与y轴的交点为(0,3),则方程ax2+bx+c=0(a≠0)的解为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣8mx+16m﹣1(m>0)与x轴的交点分别为A(x1 , 0),B(x2 , 0).
(1)求证:抛物线总与x轴有两个不同的交点;
(2)若AB=2,求此抛物线的解析式.
(3)已知x轴上两点C(2,0),D(5,0),若抛物线y=mx2﹣8mx+16m﹣1(m>0)与线段CD有交点,请写出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+(m﹣1)x+m与y轴交点坐标是(0,3).
(1)求出m的值并画出这条抛物线; 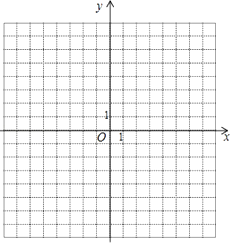
(2)求抛物线与x轴的交点和抛物线顶点的坐标;
(3)当x取什么值时,y的值随x值的增大而减小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(2,3),B(1,1),C(4,1),M(6,3).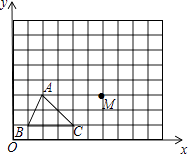
(1)将△ABC平原得到△A1B1C1 , 其中点A,B,C的对应点分别是A1 , B1 , C1 , 且点A1的坐标是(3,6),在图中画出△A1B1C1 .
(2)将(1)中的△A1B1C1绕点M顺时针旋转90°,画出旋转后的△A2B2C2(其中点A2 , B2 , C2的对应点分别是A1 , B1 , C1),并写出点A2 , B2 , C2的坐标.
(3)(2)中的△A2B2C2能通过旋转△ABC得到吗?若能,请写出旋转的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函y=ax2+bx+c(a≠0)图象的一部分,对称轴为直线x= ![]() ,且经过点(2,0),下列说法: ①abc<0;
,且经过点(2,0),下列说法: ①abc<0;
②a+b=0;
③4a+2b+c<0;
④若(﹣2,y1),(﹣3,y2)是抛物线上的两点,则y1<y2 ,
其中说法正确的是( )
A.①②④
B.③④
C.①③④
D.①②
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com