
【题目】已知如图,⊙O的直径AB与弦AC的夹角∠A=30°,AC=CP. 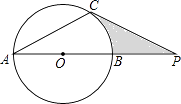
(1)求证:CP是⊙O的切线;
(2)若AB=4 ![]() ,求图中阴影部分的面积.
,求图中阴影部分的面积.
【答案】
(1)解:如图,连接OC;
∵OA=OC,AC=CP,
∴∠A=∠OCA=30°,∠P=∠A=30°,
∴∠POC=∠A+∠OCA=60°,
∴∠OCP=180°﹣60°﹣30°=90°,
∴CP是⊙O的切线
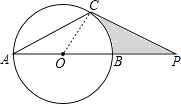
(2)解:∵AB=4 ![]() ,
,
∴OC=OB=2 ![]() ,
,
∴PC= ![]() =6
=6
∴S△OCP= ![]() OCPC
OCPC
= ![]() ×2
×2 ![]() 6=6
6=6 ![]() ,
,
S扇形OBC= ![]() =2π,
=2π,
∴图中阴影部分的面积=6 ![]() ﹣2π
﹣2π
【解析】(1)如图,连接OC;运用已知条件证明∠OCP=90°,即可解决问题.(2)分别求出△OCP、扇形OCB的面积,即可解决问题.
【考点精析】本题主要考查了切线的判定定理和扇形面积计算公式的相关知识点,需要掌握切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)才能正确解答此题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(﹣1,0)和点(0,﹣3),且顶点在第四象限,设P=a+b+c,则P的取值范围是( ) 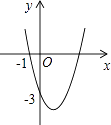
A.﹣3<P<﹣1
B.﹣6<P<0
C.﹣3<P<0
D.﹣6<P<﹣3
查看答案和解析>>
科目:初中数学 来源: 题型:
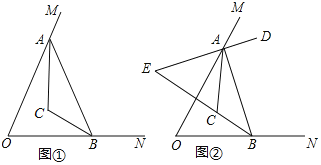
【题目】如图![]() ,
,![]() ,点A、B在
,点A、B在![]() 的两条边上运动,
的两条边上运动,![]() 与
与![]() 的平分线交于点C.
的平分线交于点C.
![]() 点A、B在运动过程中,
点A、B在运动过程中,![]() 的大小会变吗?如果不会,求出
的大小会变吗?如果不会,求出![]() 的度数;如果会,请说明理由.
的度数;如果会,请说明理由.
![]() 如图
如图![]() ,AD是
,AD是![]() 的平分线,AD的反向延长线交BC的延长线于点E,点A、B在运动过程中,
的平分线,AD的反向延长线交BC的延长线于点E,点A、B在运动过程中,![]() 的大小会变吗?如果不会,求出
的大小会变吗?如果不会,求出![]() 的度数;如果会,请说明理由.
的度数;如果会,请说明理由.
![]() 若
若![]() ,请直接写出
,请直接写出![]() ______;
______;![]() ______.
______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个铝质三角形框架三条边长分别为24cm、30cm、36cm,要估做一个与它相似的铝质三角形框架,现有长为27cm、45cm的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边.截法有( )
A.0种
B.1种
C.2种
D.3种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A、B、C在数轴上对应的数为![]() ,且
,且![]() ,多项式
,多项式![]() 是关于字母x,y的五次多项式.
是关于字母x,y的五次多项式.
(1)则a=__,b=__,c=__;并将这三数在数轴上所对应的点A、B、C表示出来;
(2)已知蚂蚁从A点出发,以每秒2cm的速度爬行,先到B点,再到C点,一共需要多少秒?
(3)数轴上在B点右边有一点D到A、B两点的距离和为11,求点D的数轴上所对应的数;(直接写出结果)
(友情提示:M、N之间距离记作|MN|,点M、N在数轴上对应的数分别为m、n,则![]() )
)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)观察下列图形与等式的关系,并填空:
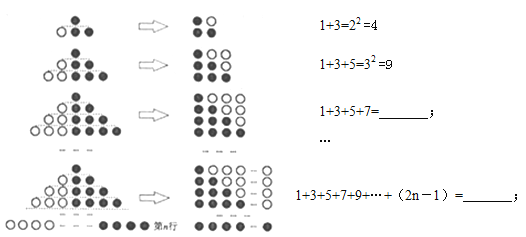
(2)利用(1)中结论,解决下列问题:
①1+3+5+…+203= ;
②计算:101+103+105+…+199;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1A2=1,∠OA1A2=90°,∠A1OA2=30°,以斜边OA2为直角边作直角三角形,使得∠A2OA3=30°,依次以前一个直角三角形的斜边为直角边一直作含30°角的直角三角形,则Rt△A2014OA2015的面积为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角△ABC中,∠ACB=90°,O是斜边AB的中点,点D,E分别在直角边AC,BC上,且∠DOE=90°,DE交OC于点P,则下列结论:①图形中全等的三角形只有两对;②△ABC的面积等于四边形CDOE的面积的两倍;③CD+CE=![]() OA;④AD2+BE2=DE2.其中正确的结论有( )
OA;④AD2+BE2=DE2.其中正确的结论有( )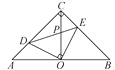
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明同学测量一个光盘的直径,他只有一把直尺和一块三角板,他将直尺、光盘和三角板如图放置于桌面上,并量出AB=3.5cm,则此光盘的直径是( )cm. 
A.7
B.![]()
C.![]()
D.14
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com