
 ��ͼ������������y=$\frac{k}{x}$��ͼ����һ�κ���y=-$\frac{1}{2}$x��ͼ����A��B���㣬��B��ĺ�����Ϊ2����P�ǵڶ������ڷ���������ͼ���ϵĶ��㣬����ֱ��AB���Ϸ���
��ͼ������������y=$\frac{k}{x}$��ͼ����һ�κ���y=-$\frac{1}{2}$x��ͼ����A��B���㣬��B��ĺ�����Ϊ2����P�ǵڶ������ڷ���������ͼ���ϵĶ��㣬����ֱ��AB���Ϸ������� ��1����B��ĺ�����Ϊ2��������һ�κ���y=-$\frac{1}{2}$x��ͼ���ϣ�������õ�B�����꣬Ȼ����뷴��������y=$\frac{k}{x}$��������ô𰸣�
��2���ɵ�P�ĺ�����Ϊ-1������õ�P�����꣬����A��B����ԭ��Գƣ�����õ�A�����꣬Ȼ�����ù��ɶ������涨�����ж���PAB��ֱ�������Σ�
��3��������P��m��-$\frac{2}{m}$����ֱ��PA�Ľ���ʽΪ��y=ax+b����ֱ��PB�Ľ���ʽΪy=px+q��Ȼ�����ô���ϵ���������ֱ��PA��PB�Ľ���ʽ�������õ�M��N�����꣬�������MN�ij����ٹ�P��PD��x�ᣬ����ΪD���̶����m��ֵ��������ô𰸣�
��� �⣺��1���ߵ�B�ĺ�����Ϊ2���ֵ�B��һ�κ���y=-$\frac{1}{2}$x��ͼ���ϣ�
���B��2��-1����
�֡ߵ�B��y=$\frac{k}{x}$�ϣ�
��k=xy=2����-1��=-2��
�෴���������Ľ���ʽΪ��y=-$\frac{2}{x}$��
��2���ߵ�P�ĺ�����Ϊ-1���ֵ�P��y=-$\frac{2}{x}$�ϣ�
��P��-1��2����
��A��B����ԭ��Գƣ�
��A��-2��1����B��2��-1����
��AB2=��-2-2��2+[1-��-1��]2=20��PB2=��2+1��2+��2+1��2=18��PA2=��2-1��2+��-1+2��2=2��
��AB2=PB2+PA2��
���PAB��ֱ�������Σ�
��3����P��m��-$\frac{2}{m}$����
��ֱ��PA�Ľ���ʽΪ��y=ax+b����ֱ��PB�Ľ���ʽΪy=px+q��
��P��m��-$\frac{2}{m}$����A��-2��1������y=ax+b�ã�$\left\{\begin{array}{l}{-\frac{2}{m}=am+b}\\{1=-2a+b}\end{array}\right.$��
��֮��$\left\{\begin{array}{l}{a=-\frac{1}{m}}\\{b=1-\frac{2}{m}}\end{array}\right.$
��ֱ��PA�Ľ���ʽΪ��y=-$\frac{1}{m}$x+1-$\frac{2}{m}$��
��M��m-2��0����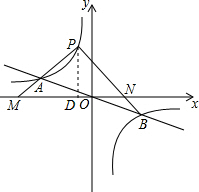 ��P��m��-$\frac{2}{m}$����B��2��-1������y=px+q�ã�$\left\{\begin{array}{l}{-\frac{2}{m}=pm+q}\\{-1=2p+q}\end{array}\right.$��
��P��m��-$\frac{2}{m}$����B��2��-1������y=px+q�ã�$\left\{\begin{array}{l}{-\frac{2}{m}=pm+q}\\{-1=2p+q}\end{array}\right.$��
��֮��$\left\{\begin{array}{l}{p=\frac{1}{m}}\\{q=-1-\frac{2}{m}}\end{array}\right.$��
��ֱ��PB�Ľ���ʽΪ��y=$\frac{1}{m}$x-1-$\frac{2}{m}$��
��N��m+2��0����
��MN=4��
����ͼ����P��PD��x�ᣬ����ΪD��
�ߡ�PMN�ǵȱ������Σ�
��PD=$\frac{\sqrt{3}}{2}$��4=2$\sqrt{3}$��
���P��������Ϊ2$\sqrt{3}$��
�֡�P��y=-$\frac{2}{x}$�ϣ�
��P��-$\frac{\sqrt{3}}{3}$��2$\sqrt{3}$������m=-$\frac{\sqrt{3}}{3}$��
��M��-$\frac{\sqrt{3}}{3}$-2��0����N��2-$\frac{\sqrt{3}}{3}$��0����
���� �������ڷ����������ۺ��⣮�����˴���ϵ����������ʽ�����ɶ������涨�����ȱ������ε������Լ�ֱ���뷴���������Ľ������⣮ע�����MN�ij���ȷ�����������ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
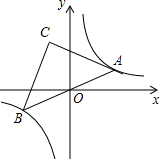 ��ͼ����A��˫����y=$\frac{8}{x}$�ڵ�һ�����ϵ�һ���㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪб��������Rt��ABC����C�ڵڶ����ޣ����ŵ�A���˶�����C��λ��Ҳ���ϵı仯����ʼ����һ����ͼ�����˶�������������Ľ���ʽΪ��������
��ͼ����A��˫����y=$\frac{8}{x}$�ڵ�һ�����ϵ�һ���㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪб��������Rt��ABC����C�ڵڶ����ޣ����ŵ�A���˶�����C��λ��Ҳ���ϵı仯����ʼ����һ����ͼ�����˶�������������Ľ���ʽΪ��������| A�� | y=$\frac{8}{x}$ | B�� | y=$\frac{16}{x}$ | C�� | y=-$\frac{16}{x}$ | D�� | y=-$\frac{8}{x}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
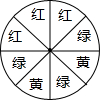 ��ͼ��һ����������ת����ת�̣�ת�����ת�̺�ת����������ɫ�Ŀ�������С��
��ͼ��һ����������ת����ת�̣�ת�����ת�̺�ת����������ɫ�Ŀ�������С��| A�� | �� | B�� | �� | C�� | �� | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ����������ͼ�У�ÿ��С�����εı߳�Ϊ1��ƽ�ơ�ABC��ʹ��Aƽ�Ƶ���D��
����������ͼ�У�ÿ��С�����εı߳�Ϊ1��ƽ�ơ�ABC��ʹ��Aƽ�Ƶ���D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
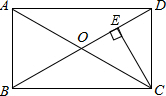 ��ͼ���ھ���ABCD�У��Խ���AC��BD���ڵ�O��CE��BD��E����֪BE��DE=3��1��BD=2$\sqrt{3}$�������ABCD���ܳ�Ϊ6+2$\sqrt{3}$��
��ͼ���ھ���ABCD�У��Խ���AC��BD���ڵ�O��CE��BD��E����֪BE��DE=3��1��BD=2$\sqrt{3}$�������ABCD���ܳ�Ϊ6+2$\sqrt{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
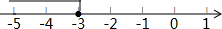 ���в���ʽ�У���⼯����ͼ��ʾ���ǣ�������
���в���ʽ�У���⼯����ͼ��ʾ���ǣ�������| A�� | -x-1��-2 | B�� | -2x-3��3 | C�� | 3x+4��-5 | D�� | x-4��7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У�D��E��F�ֱ���AB��AC��BC���ϵĵ㣬��$\frac{AD}{BD}$=$\frac{AE}{CE}$=$\frac{1}{2}$�����ı���ADFE���ABC�����֮��Ϊ$\frac{1}{3}$��
��ͼ���ڡ�ABC�У�D��E��F�ֱ���AB��AC��BC���ϵĵ㣬��$\frac{AD}{BD}$=$\frac{AE}{CE}$=$\frac{1}{2}$�����ı���ADFE���ABC�����֮��Ϊ$\frac{1}{3}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-1��-1�� | B�� | ��-1��0�� | C�� | ��-2��-1�� | D�� | ��-3��0�� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com