
【题目】如图,A(0,1),M(3,2),N(4,4), 动点P从点A出发,沿y
轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=-x+b也随之移动,设移动时间为t 秒.(直线y = kx+b平移时k不变)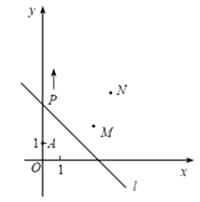
(1)当t=3时,求l 的解析式;
(2)若点M,N位于l 的异侧,确定t 的取值范围.
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一次函数y=ax+b(a≠0)的图形与反比例函数y=![]() (k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=
(k≠0)的图象交于第二、四象限内的A、B两点,与y轴交于C点,过点A作AH⊥y轴,垂足为H,OH=3,tan∠AOH=![]() ,点B的坐标为(m,﹣2).
,点B的坐标为(m,﹣2).
(1)求△AHO的周长;
(2)求该反比例函数和一次函数的解析式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市商店为了对某种商品促销,将定价为3元的商品,以下列方式优惠销售:若购买不超过5件,按原价付款;若一次性购买5件以上,超过部分打八折.如果用27元钱,最多可以购买该商品( )件
A. 9B. 10C. 11D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A(x1 , y1)是一次函数y=﹣x+b+1图象上一点,若x1<0,y1<0,则b的取值范围是( )
A.b<0
B.b>0
C.b>﹣1
D.b<﹣1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣(x﹣1)2+c与x轴交于A,B(A,B分别在y轴的左右两侧)两点,与y轴的正半轴交于点C,顶点为D,已知A(﹣1,0).
(1)求点B,C的坐标;
(2)判断△CDB的形状并说明理由;
(3)将△COB沿x轴向右平移t个单位长度(0<t<3)得到△QPE.△QPE与△CDB重叠部分(如图中阴影部分)面积为S,求S与t的函数关系式,并写出自变量t的取值范围.
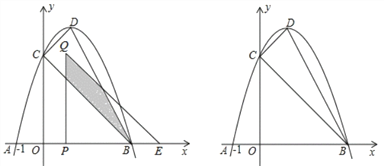
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知某小区的两幢10层住宅楼间的距离为AC="30" m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3 m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α .

(1) 用含α的式子表示h(不必指出α的取值范围);
(2) 当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光 ?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得图形与原图形相比( )
A. 向右平移了3个单位长度B. 向左平移了3个单位长度
C. 向上平移了3个单位长度D. 向下平移了3个单位长度
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=kx+b与反比例函数y=![]() (x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(x<0)的图象交于点A(﹣1,m),与x轴交于点B(1,0)
(1)求m的值;
(2)求直线AB的解析式;
(3)若直线x=t(t>1)与直线y=kx+b交于点M,与x轴交于点N,连接AN,S△AMN=![]() ,求t的值.
,求t的值.
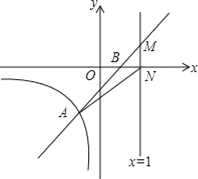
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com