
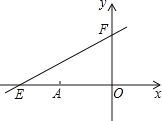
【题目】如图,直线y=kx+6与x、y轴分别交于E、F.点E坐标为(﹣8,0),点A的坐标为(﹣6,0),P(x,y)是直线y=kx+6上的一个动点.
(1)求k的值;
(2)若点P是第二象限内的直线上的一个动点,当点P运动过程中,试写出三角形OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置时,三角形OPA的面积为![]() ,并说明理由.
,并说明理由.
【答案】(1)k的值为![]() ;
;
(2)三角形OPA的面积S与x的函数关系式为S=![]() x+18(﹣8<x<0);
x+18(﹣8<x<0);
(3)当点P的坐标为P(﹣5,![]() )或P(﹣11,﹣
)或P(﹣11,﹣![]() )时,三角形OPA的面积为
)时,三角形OPA的面积为![]() .
.
【解析】试题分析: (1)将点E的坐标(-8,0)代入直线y=kx+6,得到关于k的方程,解方程即可求出k的值;
(2)由点A的坐标为(-6,0)得到OA=6,求△OPA的面积时,可看作以OA为底边,高是P点的纵坐标的绝对值.再根据三角形的面积公式表示出△OPA的面积,从而求出其关系式;根据P点运动的范围可求出自变量x的取值范围;
(3)根据三角形的面积公式,由△OPA的面积为![]() ,列出关于点P的纵坐标y的方程,解方程求出y的值,再代入直线的解析式求出x的值,即可得到P点的坐标.
,列出关于点P的纵坐标y的方程,解方程求出y的值,再代入直线的解析式求出x的值,即可得到P点的坐标.
试题解析:
(1)∵点E(﹣8,0)在直线y=kx+6上,
∴0=﹣8k+6,∴k=![]() ;
;
(2)∵k=![]() ,∴直线的解析式为:y=
,∴直线的解析式为:y=![]() x+6,
x+6,
∵点P(x,y)是第二象限内的直线y=![]() x+6上的一个动点,
x+6上的一个动点,
∴y=![]() x+6>0,﹣8<x<0.
x+6>0,﹣8<x<0.
∵点A的坐标为(﹣6,0),
∴OA=6,
∴S=![]() OA|yP|=
OA|yP|=![]() ×6×(
×6×(![]() x+6)=
x+6)=![]() x+18.
x+18.
∴三角形OPA的面积S与x的函数关系式为:S=![]() x+18(﹣8<x<0);
x+18(﹣8<x<0);
(3)∵三角形OPA的面积=![]() OA|yP|=
OA|yP|=![]() ,P(x,y),
,P(x,y),

∴![]() ×6×|y|=
×6×|y|=![]() ,
,
解得|y|=![]() ,
,
∴y=±![]() .
.
当y=![]() 时,
时,![]() =
=![]() x+6,
x+6,
解得x=﹣5,故P(﹣5,![]() );
);
当y=﹣![]() 时,﹣
时,﹣![]() =
=![]() x+6,
x+6,
解得x=﹣11,故P(﹣11,﹣![]() );
);
综上可知,当点P的坐标为P(﹣5,![]() )或P(﹣11,﹣
)或P(﹣11,﹣![]() )时,三角形OPA的面积为
)时,三角形OPA的面积为![]() .
.
点睛:此题属于一次函数综合题,涉及 的知识有:待定系数法求一次函数解析式,三角形面积,坐标与图形性质,熟练掌握待定系数法是解本题的关键.


科目:初中数学 来源: 题型:
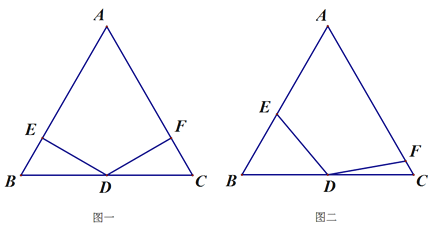
【题目】在等边△ABC中,点D是线段BC的中点,∠EDF=120°,线段DE与线段AB相交于点E.线段DF与线段AC相交于点F.
(1)如图一,若DF⊥AC,请直接写出DE与AB的位置关系;
(2)请判断DE与DF的数量关系.并写出推理过程.
(3)如图二,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F. (2)中的结论还成立吗?若成立,写出证明过程,若不成立,说明理由.
(4)在∠EDF绕点D顺时针旋转过程中,直接用等式表示线段BE、CF、AB之间的数量关系。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年6月13日,2016——2017赛季NBA总决赛第五场金州勇士队129:120战胜克利夫兰骑士队,赢得了总冠军,凯文·杜兰特表现抢眼,荣膺总决赛MVP,总决赛中凯文·杜兰特和勒布朗·詹姆斯每场得分数据如下:
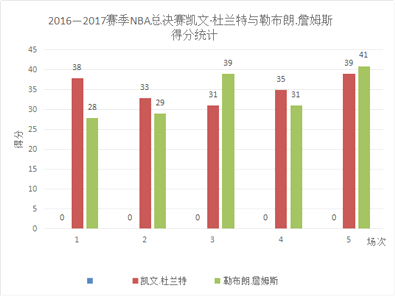
(1)求两名队员得分数的平均数.
(2)求凯文·杜兰特五场比赛得分的中位数.
(3)篮球迷小明同学已经求出了勒布朗·詹姆斯五场得分的方差为S2=28.64,凯文·杜兰特五场比赛得分的方差为S2=8.96,请帮他说明哪位运动员发挥更稳定.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com