
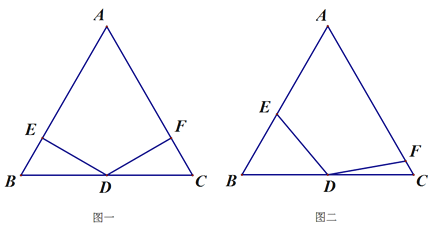
����Ŀ���ڵȱߡ�ABC�У���D���߶�BC���е㣬��EDF=120�㣬�߶�DE���߶�AB�ཻ�ڵ�E.�߶�DF���߶�AC�ཻ�ڵ�F.
��1����ͼһ����DF��AC����ֱ��д��DE��AB��λ�ù�ϵ��
��2�����ж�DE��DF��������ϵ.��д����������.
��3����ͼ��������1���еġ�EDF�Ƶ�D˳ʱ����תһ���ĽǶȣ�DF�����߶�AC�ཻ�ڵ�F. ��2���еĽ��ۻ���������������д��֤�����̣�����������˵������.
��4���ڡ�EDF�Ƶ�D˳ʱ����ת�����У�ֱ���õ�ʽ��ʾ�߶�BE��CF��AB֮���������ϵ��
���𰸡���1��DE��AB����2��DE=DF ֤������������3������.֤������������4��BE+CF=![]()
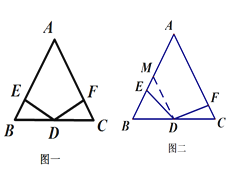
�������������������1��DE��AB�������ı��ε��ڽǺͶ���������á�AED=90�㣬����DE��AB����2�������ٿ���ͨ��AAS֤����BED�ա�CFD���ó����ۣ����� ��Ҳ��������ADͨ���������������ߺ�һ�ó�ADƽ�֡�BAC�����ý�ƽ�������ʶ����ó�����3��������֤���������ٿ��Իָ���ͼһ����ͼһ�Ļ�����֤��ȫ�ȵó����ۣ�������Ҳ����ȡAB�е�M������DM֤����EDM�ա�FDC��������4��ȡAB�е�M������DM֤����EDM�ա�FDC���ɵý���.
���������
��1��DE��AB
��2��DE=DF ֤�����ٿ���ͨ��AAS֤����BED�ա�CFD���ó�����
��Ҳ��������ADͨ���������������ߺ�һ�ó�ADƽ�֡�BAC�����ý�ƽ�������ʶ����ó�.
����.֤���ٿ��Իָ���ͼһ����ͼһ�Ļ�����֤��ȫ�ȵó�����.
��Ҳ����ȡAB�е�M������DM֤����EDM�ա�FDC����.
��4��BE+CF=![]()


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͥ���̳�����4����4000Ԫ������һ��������ɼ������к�ܿ����꣬��װ����5�³��ֹ���ͬ�������ĸÿ���£����ڵڶ������½���ʱ�۸�ȵ�һ�����½���ʱ�۸������20Ԫ������ڶ������½�������5000Ԫ��
��1����һ�����½���ʱ�ļ۸��Ƕ��٣�
��2����һ�������ۼ�Ϊ120Ԫ/����Ϊ��֤�ڶ������µ������ʲ����ڵ�һ�����µ������ʣ���ô�ڶ�������ÿ���ۼ������Ƕ���Ԫ��
����ʾ������=�ۼ����ɱ���������=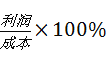 ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����P����a+2b��2��Q��8ab����P��Q�Ĵ�С��ϵΪ��������
A.P��QB.P��QC.P��QD.P��Q
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=-2(x-1)2�Ķ�������ͶԳ���ֱ���( )
A. (-1��0)��ֱ��x=-1 B. (1��0)��ֱ��x=1
C. (0��1)��ֱ��x=-1 D. (0��1)��ֱ��x=1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ���м�����Գ�ͼ�Σ��������ĶԳ�ͼ�ε��ǣ� ��
A. �ȱ������� B. ƽ���ı��� C. ������ D. �������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
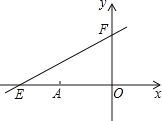
����Ŀ����ͼ��ֱ��y=kx+6��x��y��ֱ���E��F����E����Ϊ����8��0������A������Ϊ����6��0����P��x��y����ֱ��y=kx+6�ϵ�һ�����㣮
��1����k��ֵ��
��2������P�ǵڶ������ڵ�ֱ���ϵ�һ�����㣬����P�˶������У���д��������OPA�����S��x�ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
��3��̽������P�˶���ʲôλ��ʱ��������OPA�����Ϊ![]() ����˵�����ɣ�
����˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ������1��2��4��4��3������Ϊ4�����������ݵ���λ���ǣ� ��
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ��y=��2x����ƽ��������λ�����õ���ֱ��Ϊ�� ��
A.y=��2��x+2��
B.y=��2��x��2��
C.y=��2x��2
D.y=��2x+2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com