
【题目】常州春秋旅行社为吸引市民组团去天水湾风景区旅游,推出了如下收费标准:

某单位组织员工去天水湾风景区旅游,共支付给春秋旅行社旅游费用27000元,请问该单位这次共有多少员工去天水湾风景区旅游?
【答案】设该单位去风景区旅游人数为x人,则人均费用为1000-20(x-25)元
由题意得 x[1000-20(x-25)]=27000
整理得x2-75x+1350=0,
解得x1=45,x2=30.
当x=45时,人均旅游费用为1000-20(x-25)=600<700,不符合题意,应舍去.
当x=30时,人均旅游费用为1000-20(x-25)=900>700,符合题意.
答:该单位去风景区旅游人数为30人.
【解析】试题分析:首先根据共支付给春秋旅行社旅游费用27 000元,确定旅游的人数的范围,然后根据每人的旅游费用×人数=总费用,设该单位这次共有x名员工去天水湾风景区旅游.即可由对话框,超过25人的人数为(x-25)人,每人降低20元,共降低了20(x-25)元.实际每人收了[1000-20(x-25)]元,列出方程求解.
试题解析:设该单位这次共有x名员工去天水湾风景区旅游.
因为1000×25=25000<27000,所以员工人数一定超过25人.
可得方程[1000-20(x-25)]x=27000.
整理得x2-75x+1350=0,
解得x1=45,x2=30.
当x1=45时,1000-20(x-25)=600<700,故舍去x1;
当x2=30时,1000-20(x-25)=900>700,符合题意.
答:该单位这次共有30名员工去天水湾风景区旅游.


科目:初中数学 来源: 题型:
【题目】如图,△ABC在平面直角坐标系中.
(1)若把△ABC向上平移2个单位长度,再向左平移1个单位长度得到△A1B1C1,写出A1,B1,C1的坐标;
(2)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E,F,G分别是AD,CD,BC上的点,且BE=EF,BE⊥EF,EG⊥BF.若FC=1,AE=2,则BG的长是( )
A.2.6
B.2.5
C.2.4
D.2.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 。
。
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=3,BC=5,点E是AD边上一点,BE=BC.
(1)求证:EC平分∠BED.
(2)过点C作CF⊥BE,垂足为点F,连接FD,与EC交于点O,求FD·EC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】线段AB两端点坐标分别为A(﹣1,4),B(4,﹣2),现将线段AB平移后点A的对应点坐标为(﹣4,2),则点B的对应点的坐标为( )
A.(1,4)
B.(1,﹣4)
C.(2,﹣5)
D.(1,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
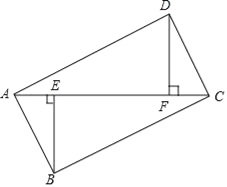
【题目】如图,在四边形ABCD中,BE⊥AC,DF⊥AC,垂足分别为E,F,BE=DF,AE=CF.
(1)求证:△AFD≌△CEB;
(2)若∠CBE=∠BAC,四边形ABCD是怎样的四边形?证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新冠状病毒战斗中,有152箱公共卫生防护用品要运到A、B两城镇,若用大小货车共15辆,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,则恰好能一次性运完这批防护用品求这大小货车各多少辆?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com