
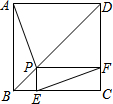
 如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP.其中,所有正确的结论是( )
如图,P为正方形ABCD的对角线BD上任一点,过点P作PE⊥BC于点E,PF⊥CD于点F,连接EF.给出以下4个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP.其中,所有正确的结论是( )| A. | ①② | B. | ①③ | C. | ①②④ | D. | ①③④ |
分析 先证明四边形PECF是矩形,得出对角线相等PC=EF,再证明△ABP≌△CBP,得出AP=PC,即可得出①正确;
延长AP交EF于N,由平行线得出∠EPN=∠BAP,由△ABP≌△CBP,得出∠BAP=∠BCP,由P、E、C、F四点共圆,得出同弧所对的圆周角相等∠PFE=∠BCP,得出∠BAP=∠BCP=∠PFE(④正确),证出∠PNE=90°,得出AP⊥EF,②正确;
由于P是动点,△APD不一定是等腰三角形,得出③错误.
解答 解:①正确;连接PC,如图所示: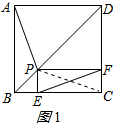
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠C=90°,∠ABP=∠CBP=45°,
∵PE⊥BC,PF⊥CD,
∴∠PEC=∠FCE=90°,
∴四边形PECF是矩形,
∴PC=EF,
在△ABP和△CBP中,$\left\{\begin{array}{l}{AB=CB}&{\;}\\{∠ABP=∠CBP}&{\;}\\{BP=BP}&{\;}\end{array}\right.$,
∴△ABP≌△CBP(SAS),
∴AP=PC,
∴AP=EF;
②④正确;延长AP交EF于N,如图2所示: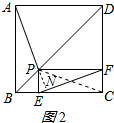
∵AB∥PE,
∴∠EPN=∠BAP,
∵△ABP≌△CBP,
∴∠BAP=∠BCP,
∵四边形PECF是矩形,
∴P、E、C、F四点共圆,
∴∠PFE=∠BCP,
∴∠BAP=∠BCP=∠PFE,
∵∠PEF+∠PFE=90°,
∴∠PEF+∠EPN=90°,
∴∠PNE=90°,
∴AP⊥EF;
③错误;
∵P是动点,
∴△APD不一定是等腰三角形;
正确的结论是①②④,
故选:C.
点评 本题考查了正方形的性质、全等三角形的判定与性质、矩形的判定与性质、四点共圆、圆周角定理;熟练掌握正方形的性质,并能进行推理论证是解决问题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=-x2+2x+3经过点A、C、A′三点.
如图,在平面直角坐标系中,平行四边形ABOC如图放置,将此平行四边形绕点O顺时针旋转90°得到平行四边形A′B′OC′.抛物线y=-x2+2x+3经过点A、C、A′三点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
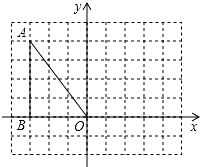 如图,已知点A(-3,4),B(-3,0),将△OAB绕原点O顺时针旋转90°,得到△OA1B1.
如图,已知点A(-3,4),B(-3,0),将△OAB绕原点O顺时针旋转90°,得到△OA1B1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
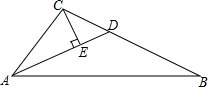 如图,已知△ABC,AD平分∠BAC,∠CAB=2∠B,CE⊥AD于E,且CB=10.(1)求AE的长;
如图,已知△ABC,AD平分∠BAC,∠CAB=2∠B,CE⊥AD于E,且CB=10.(1)求AE的长;查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.79×103 | B. | 3.79×104 | C. | 3.79×105 | D. | 0.379×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 从1,2,3,4,5这五个数中,任选两个数,所得两数的平方和是一个整数 | |
| B. | 从1,2,3,4,5这五个数中,任选两个数,所得两数的平方和是一个正整数的平方 | |
| C. | 从1,2,3,4,5这五个数中,任选两个数,所得两数的平方和是一个正整数的立方 | |
| D. | 从1,2,3,4,5这五个数中,任选两个数,所得两数的平方和是一个正整数的四次方 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com