
【题目】在△ABC中,AB=AC,点D,E分别在AC,AB上,下列条件中,不能使BD=CE的是( )
A. BD,CE为AC,AB上的高
B. BD,CE都为△ABC的角平分线
C. ∠ABD=![]() ∠ABC,∠ACE=
∠ABC,∠ACE=![]() ∠ACB
∠ACB
D. ∠ABD=∠BCE
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AC,BD为对角线,AB=BC=AC=BD,则∠ADC的大小为( )
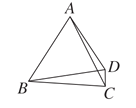
A. 120°B. 135°C. 145°D. 150°
查看答案和解析>>
科目:初中数学 来源: 题型:
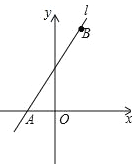
【题目】如图,已知直线l1经过点A(﹣1,0)和点B(1,4)
(1)求直线l1的表达式;
(2)若点P是x轴上的点,且△APB的面积为8,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
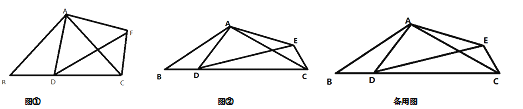
【题目】已知如图,在△ABC中,AB=AC,点D是线段BC上一个动点,以AD为腰在线段AD的右侧作△ADE,且AD=AE。
(1)如图①,当∠BAC=∠DAE=90°时,试判断线段BD和CE有什么关系,并给出证明:
(2)在(1)的条件下,若BC=4.试判断四边形ADCE的面积是否发生变化,若不变,求出四边形ADCE的面积;若变化,请说明理由;
(3)如图②,若∠BAC=∠DAE=120°,BC=4,试探索△DCE的面积是否存在最大值,若存在,求出此时∠DEC的度数,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△DEF都是等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合.将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,射线EF与线段AB相交于点G,与射线CA相交于点Q.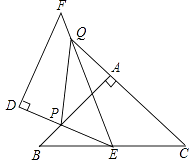
(1)求证:△BPE∽△CEQ;
(2)求证:DP平分∠BPQ;
(3)当BP=a,CQ= ![]() a,求PQ长(用含a的代数式表示).
a,求PQ长(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是矩形ABCD的边AD上的一动点,矩形的两条边AB,BC的长分别是6和8,则点P到矩形的两条对角线距离之和PE+PF是( )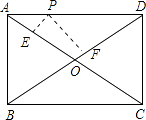
A.4.8
B.5
C.6
D.7.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,连接BF,EF,恰有BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作EF的垂线,交EF于点M,交DA的延长线于点N,连接NG.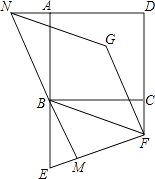
(1)求证:BE=2CF;
(2)试猜想四边形BFGN是什么特殊的四边形,并对你的猜想加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(8分) 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁处一块面积为300cm2的长方形纸片.(1)请帮小丽设计一种可行的裁剪方案;
(2)若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案,若不能,请简要说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com