
【题目】如图,在△ABC中,D为BC的中点,E,F分别是AB,AC上的点,且DE⊥DF.
求证:BE+CF>EF. 
【答案】证明:如图,延长ED至点M,使DM=ED,连接MC,MF,则EF=FM .
∵BD=CD,ED=DM,∠EDB=∠CDM,
∴△BDE≌△CDM(SAS).
∴BE=CM.
∵CF+CM>MF,
∴BE+CF>EF.
【解析】延长ED至点M,使DM=ED,连接MC,MF,根据中垂线的性质得出 :EF=FM ,然后利用SAS判断出△BDE≌△CDM ,根据全等三角形的对应边相等得出BE=CM ,根据三角形三边之间的关系得出CF+CM>MF,然后等量代换得出BE+CF>EF. 。
【考点精析】认真审题,首先需要了解三角形三边关系(三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边),还要掌握线段垂直平分线的性质(垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y=(x-1)2+1与y轴交于点A,过点A与点(1,3)的直线与C1交于点B
(1) 求直线AB的函数表达式
(2) 如图1,若点P为直线AB下方的C1上一点,求点P到直线AB的距离的最大值
(3) 如图2,将直线AB绕点A顺时针旋转90°后恰好经过C1的顶点C,沿射线AC的方向平移抛物线C1得到抛物线C2,C2的顶点为D,两抛物线相交于点E.设交点E的横坐标为m.若∠AED=90°,求m的值


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知线段AB的两个端点分别是A(4,﹣1),B(1,1)将线段AB平移后得到线段A′B′,若点A的坐标为(﹣2,2),则点B′的坐标为( )
A.(﹣5,4)
B.(4,3)
C.(﹣1,﹣2)
D.(﹣2,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算:ab=a(1﹣b).若a,b是方程x2﹣x+![]() m=0(m<0)的两根,则bb﹣aa的值为( )
m=0(m<0)的两根,则bb﹣aa的值为( )
A. 0 B. 1 C. 2 D. 与m有关
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC 中,∠C=90°,BC=3,AC=4.现在要将交ABC 扩充成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后等腰三角形的周长.
赵佳同学是这样操作的:如图 1 所示,延长BC 到点 D,使CD=BC,连接AD.所以,△ADB 为符合条件的三角形.则此时△ADB的周长为____________.
请你在图2、图3中再设计两种扩充方案,并直接写出扩充后等腰三角形的周长.
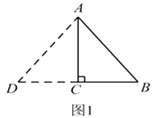
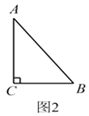
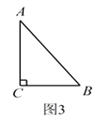
图2的周长:______________;图3的周长:______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请认真观察图形,解答下列问题:
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);并由此得到怎样的等量关系?请用等式表示;
(2)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值; ②a-b的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com