
【题目】已知抛物线C1:y=(x-1)2+1与y轴交于点A,过点A与点(1,3)的直线与C1交于点B
(1) 求直线AB的函数表达式
(2) 如图1,若点P为直线AB下方的C1上一点,求点P到直线AB的距离的最大值
(3) 如图2,将直线AB绕点A顺时针旋转90°后恰好经过C1的顶点C,沿射线AC的方向平移抛物线C1得到抛物线C2,C2的顶点为D,两抛物线相交于点E.设交点E的横坐标为m.若∠AED=90°,求m的值


【答案】(1) y=x+2(2)![]() (3)m=1+
(3)m=1+![]()
【解析】(1) y=x+2
(2) 设P(a,a2-2a+2)
过点P作PQ∥y交轴交AB于Q
∴Q(a,a+2)
∴PQ=(a+2)-(a2-2a+2)=-a2+3a=![]()
当![]() 时,PQ有最大值为
时,PQ有最大值为![]()
过点P作PM⊥AB于M
∵直线AB与竖直方向的夹角为45°
∴△PQM为等腰直角三角形
∴PM=![]()
即P到AB的距离的最大值为![]()
方法2:P在平行于AB且于抛物线相切的切点处
(3) 直线AD的解析式为y=-x+2
设D(n,-n+2)
∴C2:y=(x-n)2-n+2
∵E(m,m2-2m+2)同时也在C2上
∴(m-n)2-n+2=m2-2m+2
整理得:(2m-n)(n-1)=0,n=2m或n=1(舍去)
∴D(2m,-2m+2)
接下来使用K字型
过点E作MN∥x轴交y轴于M,过点D作DN⊥MN于N
∴△DNE∽△EMA
∴DN·AM=ME·EN
即[(m2-2m+2)-(-2m+2)]·[(m2-2m+2)-2]=m2,m2-2m-1=0
解得![]()
∵m>0
∴![]()


科目:初中数学 来源: 题型:
【题目】已知正方形 ![]() 的对角线
的对角线 ![]() ,
, ![]() 相交于点
相交于点 ![]() .
.
(1)如图1, ![]() ,
, ![]() 分别是
分别是 ![]() ,
, ![]() 上的点,
上的点, ![]() 与
与 ![]() 的延长线相交于点
的延长线相交于点 ![]() .若
.若 ![]() ,求证:
,求证: ![]() ;
;
(2)如图2, ![]() 是
是 ![]() 上的点,过点
上的点,过点 ![]() 作
作 ![]() ,交线段
,交线段 ![]() 于点
于点 ![]() ,连结
,连结 ![]() 交
交 ![]() 于点
于点 ![]() ,交
,交 ![]() 于点
于点 ![]() .若
.若 ![]() ,
,
①求证: ![]() ;
;
②当 ![]() 时,求
时,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
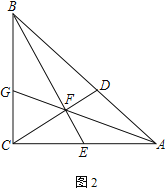
【题目】△ABC中,∠ACB=90°,点E为AC的中点,CD⊥BE交AB于D点,交BE于点F
(1) 如图1,若AC=2BC,求证:AD=2BD
(2) 如图2,若∠ACD=30°,连AF并延长交BC于G点,求![]() 的值
的值
(3) 在(1)的条件下,若AC=4,以AB为边作等腰直角三角形ABM(点M与点C在AB异侧),直接写出CM的长

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】H7N9型禽流感是一种新型禽流感,于2013年3月底在上海和安徽两地率先发现.H7N9型禽流感是全球首次发现的新亚型流感病毒,其细胞的直径约为0.000000106m,用科学记数法表示这个数是( )
A.0.106×10﹣6m
B.0.106×106m
C.1.06×10﹣7m
D.1.06×107m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某运动队欲从甲、乙两名优秀选手中选一名参加全省射击比赛,该运动队预先对这两名选手进行了8次测试,测得的成绩如表:
次数 | 选手甲的成绩(环) | 选手乙的成绩(环) |
1 | 9.6 | 9.5 |
2 | 9.7 | 9.9 |
3 | 10.5 | 10.3 |
4 | 10.0 | 9.7 |
5 | 9.7 | 10.5 |
6 | 9.9 | 10.3 |
7 | 10.0 | 10.0 |
8 | 10.6 | 9.8 |
根据统计的测试成绩,请你运用所学过的统计知识作出判断,派哪一位选手参加比赛更好?为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com