
����Ŀ������̽����
��ͼ1����ACB����DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
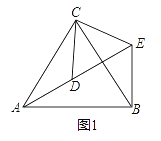
��1��֤����AD=BE��
��2�����AEB�Ķ�����
�����ʽ��
��3����ͼ2����ACB����DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90������A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE���������������AEB�Ķ������������ж��߶�CM��AE��BE֮���������ϵ����˵�����ɣ�
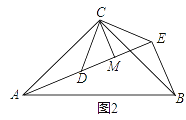
���𰸡���1������⣻��2��60������3��������90����������AE=BE+2CM�����ɼ����.
��������
��1����������ACB�͡�DCE��Ϊ�ȱ������Σ���֤��ACD�ա�BCE���Ӷ��õ���Ӧ����ȣ���AD=BE��
��2�����ݡ�ACD�ա�BCE���ɵá�ADC=��BEC���ɵ�A��D��E��ͬһֱ���ϣ��������ADC=120�����Ӷ����������AEB�Ķ�����
��3�����������ȸ��ݡ�ACB�͡�DCE��Ϊ����ֱ�������Σ��ɵ�AC=BC��CD=CE����ACB=��DCE=90�����ݴ��жϳ���ACD=��BCE��Ȼ�����ȫ�������ε��ж��������жϳ���ACD�ա�BCE�������жϳ�BE=AD����BEC=��ADC�������жϳ���AEB�Ķ���Ϊ90��������������DCE=90����CD=CE��CM��DE���ɵ�CM=DM=EM������DE=DM+EM=2CM���ݴ��жϳ�AE=BE+2CM��
�⣺��1����ͼ1��

�ߡ�ACB����DCE��Ϊ�ȱ������Σ�
��CA=CB��CD=CE����ACB=��DCE=60����
���ACD=��BCE��
����ACD����BCE��
���ACD�ա�BCE��SAS����
��AD=BE��
��2����ͼ1���ߡ�ACD�ա�BCE��
���ADC=��BEC��
�ߡ�DCEΪ�ȱ������Σ�
���CDE=��CED=60����
�ߵ�A��D��E��ͬһֱ���ϣ�
���ADC=120����
���BEC=120����
���AEB=��BEC-��CED=60����
��3����������ͼ2��
�ߡ�ACB����DCE��Ϊ����ֱ�������Σ�
��AC=BC��CD=CE����ACB=��DCE=90������CDE=��CED=45����
���ACB-��DCB=��DCE-��DCB��
����ACD=��BCE��
����ACD����BCE�� ��
��
���ACD�ա�BCE��SAS����
��BE=AD����BEC=��ADC��
�ߵ�A��D��E��ͬһֱ���ϣ�
���ADC=180-45=135����
���BEC=135����
���AEB=��BEC-��CED=135��-45��=90����
�ʴ�Ϊ��90����
��������ͼ2���ߡ�DCE=90����CD=CE��CM��DE��
��CM=DM=EM��
��DE=DM+EM=2CM��
�ߡ�ACD�ա�BCE����֤����
��BE=AD��
��AE=AD+DE=BE+2CM��
�ʴ�Ϊ��AE=BE+2CM��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� �Ķ�����IJ��ϣ������������
���ϣ����ⷽ��x4-3x2+2=0����
�⣺��x2=y��ԭ���̱�Ϊy2-3y+2=0����y-1����y-2��=0����y=1��y=2
��y=1ʱ����x2=1�����x=��1��
��y=2ʱ����x2=2�����x=��![]()
����������ԭ���̵Ľ�Ϊx1=1��x2=-1��x3=![]() ��x4=-
��x4=-![]()
���⣺��1�����������̲��õ���ѧ˼�뷽����______
A���Ӽ���Ԫ�� B��������Ԫ�� C����Ԫ�� D������ϵ����
��2���������Ƶķ����ⷽ�̣���x2-2x��2-x2+2x-6=0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=x2+bx+c����A����4����3������y�ύ�ڵ�B���Գ�����x=��3�������������⣺
(1)�������ߵĽ���ʽ.
(2)����x��ƽ�е�ֱ���������߽���C��D���㣬��C�ڶԳ�����࣬��CD=8�����BCD�����.ע��������y=ax2+bx+c��a��0���ĶԳ�����x=��![]() .
.
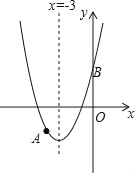
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ͼ��1������֪������ABC�У���BAC��90����AB=AC��ֱ��m������A��BD��ֱ��m, CE��ֱ��m,����ֱ�Ϊ��D��E.֤��:DE=BD+CE.
��2�� ��ͼ��2��������1���е�������Ϊ������ABC�У�AB=AC��D��A��E���㶼��ֱ��m��,��������BDA=��AEC=��BAC=![]() ,����
,����![]() Ϊ������ǻ�۽�.���ʽ���DE=BD+CE�Ƿ����?�����,�������֤��;��������,��˵������.
Ϊ������ǻ�۽�.���ʽ���DE=BD+CE�Ƿ����?�����,�������֤��;��������,��˵������.
��3����չ��Ӧ�ã���ͼ��3����D��E��D��A��E��������ֱ��m�ϵ������㣨D��A��E���㻥���غϣ�,��FΪ��BACƽ�����ϵ�һ��,����ABF����ACF��Ϊ�ȱ������Σ�����BD��CE,����BDA=��AEC=��BAC�����ж���DEF����״.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijһ�������������б�ʱ���мס����������̶�Ͷ�꣬�����㣺�ӵ�������������Ҫ60�죬���ɼ�����20�죬ʣ�µĹ����ɼס��Һ���24�����ɣ�
��1���Ҷӵ�������������Ҫ�����죿
��2����ʩ��һ�죬�踶���̿�3.5��Ԫ���Ҷ�ʩ��һ���踶���̿�2��Ԫ�����ù��̼ƻ���70������ɣ��ڲ������ƻ�������ǰ���£����ɼӻ��Ҷӵ�����ɹ���ʡǮ�������ɼ�������ȫ�̺�����ɸù���ʡǮ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
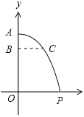
����Ŀ��ij�����������ص���Ȼ�ֺ����վ�ij���ӷ�����������Ͷ���ʣ���֪��Ͷ�����뿪�ɻ����ڿ����������߽��䣬�����߶���Ϊ���պ���![]() ����ͼ��ʾ�������Ͷ�����뿪
����ͼ��ʾ�������Ͷ�����뿪![]() ��������Ĵ�ֱ�߶�
��������Ĵ�ֱ�߶�![]() ��ʱ������
��ʱ������![]() ����ˮƽ����
����ˮƽ����![]() �ף���ôҪʹ�ɻ��ڴ�ֱ�߶�
�ף���ôҪʹ�ɻ��ڴ�ֱ�߶�![]() �ĸ߿ս��п�Ͷ������ǡ��ȷ�����ھ����
�ĸ߿ս��п�Ͷ������ǡ��ȷ�����ھ����![]() �����ɻ���
�����ɻ���![]() ����ˮƽ����
����ˮƽ����![]() ӦΪ________�ף�
ӦΪ________�ף�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijʳƷ���۵�ΪʳƷ������һ�������δ�۳�����������˻س��ң���ͳ������������֣���������������۵���Ϊ7��ʱ��ÿ������160�����ڴ˻����ϣ�����ÿ���1��ʱ�������۵�ÿ��ͻ�������20���������������������۵���Ϊx��(ÿ������ijɱ���5��)�����۵�ÿ�������������������Ϊy�ǣ�
(1)�ú�x�Ĵ���ʽ�ֱ��ʾ��ÿ����������������������������
(2)��x��y֮��ĺ�����ϵʽ��
(3)��������������۵��۶�Ϊ����ʱ�������۵�ÿ���������������õ���������������Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ھ�կ��������ţ�����⣬����Э�飬ÿ��������![]() Ԫ������ţ��ͷ�ţ��
Ԫ������ţ��ͷ�ţ��![]() �������ţ��ͻ�ţ�������֮��Ϊ
�������ţ��ͻ�ţ�������֮��Ϊ![]() ����֪ÿ����ţ����ۼ۱�ÿ���ţ����ۼ۶�
����֪ÿ����ţ����ۼ۱�ÿ���ţ����ۼ۶�![]() Ԫ��Ԥ�Ƶ����ȫ�����꣮
Ԫ��Ԥ�Ƶ����ȫ�����꣮
��1����С��Ԥ��ÿ��ӯ��������![]() Ԫ������ţ��ÿ������������Ԫ��
Ԫ������ţ��ÿ������������Ԫ��
��2������ţ��ͻ�ţ����ڣ�1��������������ͼ۸����ۣ���8�·���Ϊ��կ�������οʹ������٣�����ţ��������С�ξ�����������ÿ�������ţ�⣬��֪��ţ��ĵ����½�![]() (����
(����![]() ) �����������DZȽ��������½���
) �����������DZȽ��������½���![]() ����ţ��ÿ���½���
����ţ��ÿ���½���![]() Ԫ�������Ƚ��������½���
Ԫ�������Ƚ��������½���![]() ������ÿ����ţ������۶�Ȼ�ţ�����۶��
������ÿ����ţ������۶�Ȼ�ţ�����۶��![]() ������
������![]() Ԫ����
Ԫ����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ1����E��BC����һ���㣨��E�����B��C�غϣ������߶�DEΪ�߳�����������DEFG��ʹ�õ�F��G����ֱ��DE���·�������AF��BF������ABFΪ����������ʱ��BE�ij�Ϊ_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com