
【题目】如图(1),![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于
于![]() ,过
,过![]() 点作与
点作与![]() 垂直的直线
垂直的直线![]() .动点
.动点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() 以每秒1个单位长度的速度向终点
以每秒1个单位长度的速度向终点![]() 运动,运动时间为
运动,运动时间为![]() 秒,同时动点
秒,同时动点![]() 从点
从点![]() 出发沿折线
出发沿折线![]() 以相同的速度运动,当点
以相同的速度运动,当点![]() 到达点
到达点![]() 时
时![]() 、
、![]() 同时停止运动.
同时停止运动.


(1)请写出![]() 的长为_______,
的长为_______,![]() 的长为_______;
的长为_______;
(2)当![]() 在
在![]() 上
上![]() 在
在![]() 上运动时,如图(2),设
上运动时,如图(2),设![]() 与
与![]() 交于点
交于点![]() ,当
,当![]() 为何值时,
为何值时,![]() 为等腰三角形?求出所有满足条件的
为等腰三角形?求出所有满足条件的![]() 值.
值.
【答案】(1)OC=2,BC=2;(2)t= ![]() 或
或![]()
【解析】
(1)求出∠B,根据直角三角形性质求出OA,求出AB,在△AOC中,根据勾股定理得出关于OC的方程,求出OC,即可得出答案;
(2)有三种情况:①OM=PM时,求出OP=2OQ,代入求出即可;②PM=OP时,此时不存在等腰三角形;③OM=OP时,过P作PG⊥ON于G,求出OG和QG的值,代入OG+QG=t2,即可求出答案.
(1)解:∵∠A=90°,∠AOB=60°,OB=2![]() ,
,![]() 的平分线
的平分线![]() 交
交![]() 于
于![]() ,
,
∴∠B=30°,
∴OA=![]()
由勾股定理得:AB=3,
∵OC平分∠AOB,
∴∠AOC=∠BOC=30°=∠B,
∴OC=BC,
在△AOC中,AO2+AC2=CO2,
∴(![]() )2+(3OC)2=OC2,
)2+(3OC)2=OC2,
∴OC=2=BC,
答:OC=2,BC=2.
(2)解:如图,∵ON⊥OB,

∴∠NOB=90°,
∵∠B=30°,∠A=90°,
∴∠AOB=60°,
∵OC平分∠AOB,
∴∠AOC=∠BOC=30°,
∴∠NOC=90°30°=60°,
①OM=PM时,
∠MOP=∠MPO=30°,
∴∠PQO=180°∠QOP∠MPO=90°,
∴OP=2OQ,
∴2(t2)=4t,
解得:t=![]()
②PM=OP时,
此时∠PMO=∠MOP=30°,
∴∠MPO=120°,
∵∠QOP=60°,
∴此时不存在;
③OM=OP时,
过P作PG⊥ON于G,
OP=4t,∠QOP=60°,
∴∠OPG=30°,
∴GO=![]() (4t),PG=
(4t),PG=![]() (4t),
(4t),
∵∠AOC=30°,OM=OP,
∴∠OPM=∠OMP=75°,
∴∠PQO=180°∠QOP∠QPO=45°,
∴PG=QG=![]() (4t),
(4t),
∵OG+QG=OQ,
∴![]() (4t)+
(4t)+![]() (4t)=t2,
(4t)=t2,
解得:t=![]()
综合上述:当t为 ![]() 或
或![]() 时△OPM是等腰三角形.
时△OPM是等腰三角形.


科目:初中数学 来源: 题型:
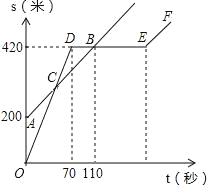
【题目】巴蜀中学的小明和朱老师一起到一条笔直的跑道上锻炼身体,到达起点后小明做了一会准备活动,朱老师先跑.当小明出发时,朱老师已经距起点200米了.他们距起点的距离s(米)与小明出发的时间t(秒)之间的关系如图所示(不完整).据图中给出的信息,解答下列问题:
(1)在上述变化过程中,自变量是______,因变量是______;
(2)朱老师的速度为_____米/秒,小明的速度为______米/秒;
(3)当小明第一次追上朱老师时,求小明距起点的距离是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,AB∥OC,A(0,3),B(a,b),C(c,0),且a,c满足![]() .点P从点A出发,以每秒1个单位长度的速度向点B运动,点Q从点O同时出发,以每秒2个单位长度的速度向点C运动,当点Q到达点C时,点P随之停止运动.设运动时间为t(秒).
.点P从点A出发,以每秒1个单位长度的速度向点B运动,点Q从点O同时出发,以每秒2个单位长度的速度向点C运动,当点Q到达点C时,点P随之停止运动.设运动时间为t(秒).

(1)B,C两点的坐标为:B ,C ;
(2)当t为何值时,四边形PQCB是平行四边形?
(3)D为线段AB的中点,求当t为何值时,△ADQ是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校把一块三角形的废地开辟为动物园,如图所示,测得AC=80m,BC=60m,AB=100m.
(1)若入口E在边AB上,且与A、B等距离,求入口E到出口C的最短距离;
(2)若线段CD是一条小渠,且点D在边AB上.点D距点A多远时,水渠的距离最短?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红旗连锁超市准备购进甲、乙两种绿色袋装食品.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) |
|
|
售价(元/袋) | 20 | 13 |
(1)求![]() 的值;
的值;
(2)要使购进的甲、乙两种绿色袋装食品共800袋的总利润(利润=售价-进价)不少于4800元,且不超过4900元,问该超市有几种进货方案?
(3)在(2)的条件下,该超市如果对甲种袋裝食品每袋优惠![]() 元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
元出售,乙种袋装食品价格不变.那么该超市要获得最大利润应如何进货?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线y=ax2﹣2ax+a+4(a<0)经过点B.

(1)求a的值,并写出抛物线的表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,
①当点M(2,n)时,求n,并求△ABM的面积.
②当点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值和此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】整体思想就是通过研究问题的整体形式从面对问题进行整体处理的解题方法.如 ,此题设“
,此题设“![]() ,
,![]() ”,得方程
”,得方程![]() ,解得
,解得![]() ,
,![]() .利用整体思想解决问题:采采家准备装修-厨房,若甲,乙两个装修公司,合做
.利用整体思想解决问题:采采家准备装修-厨房,若甲,乙两个装修公司,合做![]() 需周完成,甲公司单独做4周后,剩下的由乙公司来做,还需
需周完成,甲公司单独做4周后,剩下的由乙公司来做,还需![]() 周才能完成,设甲公司单独完成需
周才能完成,设甲公司单独完成需![]() 周,乙公司单独完成需
周,乙公司单独完成需![]() 周,则得到方程_______.利用整体思想 ,解得__________.
周,则得到方程_______.利用整体思想 ,解得__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com