
ЁОЬтФПЁПШчЭМЃЌжБЯпlЃКy=Љ3x+3гыxжсЁЂyжсЗжБ№ЯрНЛгкAЁЂBСНЕуЃЌХзЮяЯпy=ax2Љ2ax+a+4ЃЈaЃМ0ЃЉОЙ§ЕуBЃЎ

ЃЈ1ЃЉЧѓaЕФжЕЃЌВЂаДГіХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉвбжЊЕуMЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌВЂЧвЕуMдкЕквЛЯѓЯоФкЃЌСЌНгAMЁЂBMЃЌ
ЂйЕБЕуMЃЈ2ЃЌnЃЉЪБЃЌЧѓnЃЌВЂЧѓЁїABMЕФУцЛ§.
ЂкЕБЕуMЕФКсзјБъЮЊmЃЌЁїABMЕФУцЛ§ЮЊSЃЌЧѓSгыmЕФКЏЪ§БэДяЪНЃЌВЂЧѓГіSЕФзюДѓжЕКЭДЫЪБЕуMЕФзјБъ.
ЁОД№АИЁПЃЈ1ЃЉa=Љ1ЃЌy=Љx2+2x+3ЃЛ
ЃЈ2ЃЉЂйn=3ЃЌSЁїABM=3ЃЛ
ЂкS =Љ![]() ЃЈmЉ
ЃЈmЉ![]() ЃЉ2+
ЃЉ2+![]() ЃЌMЁфЕФзјБъЮЊЃЈ
ЃЌMЁфЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉЃЌ SШЁЕУзюДѓжЕ
ЃЉЃЌ SШЁЕУзюДѓжЕ![]() ЃЎ
ЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉСювЛДЮКЏЪ§x=0ЃЌЕУГіBЕФзјБъЃЌНЋBЕФзјБъДњШыЖўДЮКЏЪ§НтЮіЪНМДПЩНтГіaЃЛЃЈ2ЃЉЂйСювЛДЮКЏЪ§y=0ЃЌЕУГіA ЕФзјБъЃЌСюЖўДЮКЏЪ§x=2ЃЌПЩЕУnМАMЕФзјБъЃЌИљОнAЁЂBЁЂMЕФзјБъПЩЧѓГіЁїABMЕФУцЛ§ЃЛЂквЊБэЪОГіЁїABMЕФУцЛ§ПЩгУИюВЙЗЈЃЌSЪЧЙигкmЕФЖўДЮКЏЪ§ЃЌвЊЧѓзюжЕЃЌНЋЖўДЮКЏЪ§НтЮіЪНаДГЩЖЅЕуЪНМДПЩ.
ЪдЬтНтЮіЃК
НтЃКЃЈ1ЃЉАбx=0ДњШыy=Ѓ3x+3ЕУy=3ЃЌ
ЁрBЃЈ0ЃЌ3ЃЉЃЌ
АбBЃЈ0ЃЌ3ЃЉДњШыy=ax2Ѓ2ax+a+4ЃЌ
Ёр3=a+4ЃЌ
Ёрa=Ѓ1ЃЌ
Ёрy=Ѓx2+2x+3ЃЛ
ЃЈ2ЃЉ Сюy=0ЕУЃК0=Ѓx2+2x+3ЃЌ
Ёрx=Ѓ1Лђ3ЃЌ
ЁрХзЮяЯпгыxжсЕФНЛЕуКсзјБъЮЊЃ1КЭ3ЃЌ
ЁпMдкХзЮяЯпЩЯЃЌЧвдкЕквЛЯѓЯоФкЃЌ
Ёр0ЃМmЃМ3ЃЌ
Сюy=0ДњШыy=Ѓ3x+3ЃЌ
Ёрx=1ЃЌ
ЁрAЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЌ
ЕБx=2ЪБЃЌДњШыy=Ѓx2+2x+3=3ЃЌдђMЃЈ2ЃЌ3ЃЉМДn=3ЃЌ
ДЫЪБMB//xжсЃЌMB=2ЃЌ SЁїABM=2ЁС3ЁС![]() =3ЃЛ
=3ЃЛ
ЃЈ3ЃЉ

ШчЭМЃЌСЌНгOM,
Сюx=mЃЌy=Ѓm2+2m+3ЃЌ
ЁрMЕФзјБъЮЊЃЈmЃЌЃm2+2m+3ЃЉЃЌ
S=SЫФБпаЮOAMBЉSЁїAOB
=SЁїOBM+SЁїOAMЉSЁїAOB
=![]() ЁСmЁС3+
ЁСmЁС3+![]() ЁС1ЁСЃЈЃm2+2m+3ЃЉЃ
ЁС1ЁСЃЈЃm2+2m+3ЃЉЃ![]() ЁС1ЁС3
ЁС1ЁС3
=Ѓ![]() m2+
m2+![]() mЃЌ
mЃЌ
ЁпS =Ѓ![]() ЃЈmЃ
ЃЈmЃ![]() ЃЉ2+
ЃЉ2+![]() ЃЌ
ЃЌ
ЁрЕБm=![]() ЪБЃЌSШЁЕУзюДѓжЕ
ЪБЃЌSШЁЕУзюДѓжЕ![]() ЃЎ
ЃЎ
ЕБm=![]() ЪБЃЌy=ЃЃЈ
ЪБЃЌy=ЃЃЈ![]() ЃЉ2+2ЁС
ЃЉ2+2ЁС![]() +3=
+3=![]() ЃЌ
ЃЌ
ЁрMЁфЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ ![]() ЃЉ.
ЃЉ.


 ЛюСІПЮЪБЭЌВНСЗЯАВсЯЕСаД№АИ
ЛюСІПЮЪБЭЌВНСЗЯАВсЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮOABCЕФСНБпOAЁЂOCЗжБ№дкxжсЁЂyжсЩЯЃЌЕуDЃЈ5ЃЌ3ЃЉдкБпABЩЯЃЌвдCЮЊжааФЃЌАбЁїCDBа§зЊ90ЁуЃЌдђа§зЊКѓЕуDЕФЖдгІЕуDЁфЕФзјБъЪЧ ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№дк
ЗжБ№дк![]() ЁЂ
ЁЂ![]() ЩЯЃЌСЌНг
ЩЯЃЌСЌНг![]() ЁЂ
ЁЂ![]() НЛгкЕу
НЛгкЕу![]() ЃЌЧв
ЃЌЧв![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃК![]() ЃЎ
ЃЎ

ЃЈ2ЃЉШчЭМ2ЃЌ![]() ЪЧ
ЪЧ![]() ЕФжаЕуЃЌЪдЬНЬж
ЕФжаЕуЃЌЪдЬНЬж![]() гы
гы![]() ЕФЮЛжУЙиЯЕЃЎ
ЕФЮЛжУЙиЯЕЃЎ

ЃЈ3ЃЉШчЭМ3ЃЌ![]() ЁЂ
ЁЂ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() ЁЂ
ЁЂ![]() ЕФжаЕуЃЌШє
ЕФжаЕуЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФУцЛ§ЃЎ
ЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЕШбќШ§НЧаЮ![]() жаЃЌ
жаЃЌ![]() БпЩЯЕФИпЧЁКУЕШгк
БпЩЯЕФИпЧЁКУЕШгк![]() БпГЄЕФвЛАыЃЌдђ
БпГЄЕФвЛАыЃЌдђ![]() ЕШгк_______ЃЎ
ЕШгк_______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() НЛ
НЛ![]() гк
гк![]() ЃЌЙ§
ЃЌЙ§![]() Еузїгы
Еузїгы![]() ДЙжБЕФжБЯп
ДЙжБЕФжБЯп![]() ЃЎЖЏЕу
ЃЎЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂбиелЯп
ГіЗЂбиелЯп![]() вдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕу
вдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШЯђжеЕу![]() дЫЖЏЃЌдЫЖЏЪБМфЮЊ
дЫЖЏЃЌдЫЖЏЪБМфЮЊ![]() УыЃЌЭЌЪБЖЏЕу
УыЃЌЭЌЪБЖЏЕу![]() ДгЕу
ДгЕу![]() ГіЗЂбиелЯп
ГіЗЂбиелЯп![]() вдЯрЭЌЕФЫйЖШдЫЖЏЃЌЕБЕу
вдЯрЭЌЕФЫйЖШдЫЖЏЃЌЕБЕу![]() ЕНДяЕу
ЕНДяЕу![]() ЪБ
ЪБ![]() ЁЂ
ЁЂ![]() ЭЌЪБЭЃжЙдЫЖЏЃЎ
ЭЌЪБЭЃжЙдЫЖЏЃЎ


ЃЈ1ЃЉЧыаДГі![]() ЕФГЄЮЊ_______ЃЌ
ЕФГЄЮЊ_______ЃЌ![]() ЕФГЄЮЊ_______ЃЛ
ЕФГЄЮЊ_______ЃЛ
ЃЈ2ЃЉЕБ![]() дк
дк![]() ЩЯ
ЩЯ![]() дк
дк![]() ЩЯдЫЖЏЪБЃЌШчЭМЃЈ2ЃЉЃЌЩш
ЩЯдЫЖЏЪБЃЌШчЭМЃЈ2ЃЉЃЌЩш![]() гы
гы![]() НЛгкЕу
НЛгкЕу![]() ЃЌЕБ
ЃЌЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЮЊЕШбќШ§НЧаЮЃПЧѓГіЫљгаТњзуЬѕМўЕФ
ЮЊЕШбќШ§НЧаЮЃПЧѓГіЫљгаТњзуЬѕМўЕФ![]() жЕЃЎ
жЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ6ЗжЃЉШчЭМЃЌдкЁїOABжаЃЌЁЯOAB=90ЁуЃЌOA=AB=6ЃЌНЋЁїOABШЦЕуOФцЪБеыЗНЯђа§зЊ90ЁуЕУЕНЁїOA1B1ЃЎ

ЃЈ1ЃЉЯпЖЮA1B1ЕФГЄЪЧЁЁ ЁЁЃЛЁЯAOB1ЕФЖШЪ§ЪЧЁЁ ЁЁЃЎ
ЃЈ2ЃЉСЌНгAA1ЃЌЧѓжЄЃКЫФБпаЮOAA1B1ЪЧЦНааЫФБпаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓОЙ§ЕуЃЈЉ1ЃЌЉ2
ЕФЭМЯѓОЙ§ЕуЃЈЉ1ЃЌЉ2![]() ЃЉЃЌЕуAЪЧИУЭМЯѓЕквЛЯѓЯоЗжжЇЩЯЕФЖЏЕуЃЌСЌНсAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊаББпзїЕШбќжБНЧШ§НЧаЮABCЃЌЖЅЕуCдкЕкЫФЯѓЯоЃЌACгыxжсНЛгкЕуDЃЌЕБ
ЃЉЃЌЕуAЪЧИУЭМЯѓЕквЛЯѓЯоЗжжЇЩЯЕФЖЏЕуЃЌСЌНсAOВЂбгГЄНЛСэвЛЗжжЇгкЕуBЃЌвдABЮЊаББпзїЕШбќжБНЧШ§НЧаЮABCЃЌЖЅЕуCдкЕкЫФЯѓЯоЃЌACгыxжсНЛгкЕуDЃЌЕБ![]() ЪБЃЌдђЕуCЕФзјБъЮЊ______ЃЎ
ЪБЃЌдђЕуCЕФзјБъЮЊ______ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
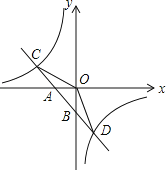
ЁОЬтФПЁПШчЭМЃЌвбжЊвЛДЮКЏЪ§y1=k1x+bЕФЭМЯѓгыxжсЁЂyжсЗжБ№НЛгкAЁЂBСНЕуЃЌгыЗДБШР§КЏЪ§y2=![]() ЕФЭМЯѓЗжБ№НЛгкCЁЂDСНЕуЃЌЕуDЃЈ2ЃЌЉ3ЃЉЃЌЕуBЪЧЯпЖЮADЕФжаЕуЃЎ
ЕФЭМЯѓЗжБ№НЛгкCЁЂDСНЕуЃЌЕуDЃЈ2ЃЌЉ3ЃЉЃЌЕуBЪЧЯпЖЮADЕФжаЕуЃЎ
ЃЈ1ЃЉЧѓвЛДЮКЏЪ§y1=k1x+bгыЗДБШР§КЏЪ§y2=![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїCODЕФУцЛ§ЃЛ
ЃЈ3ЃЉжБНгаДГі![]() ЪБздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ЪБздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ЃЈ4ЃЉЖЏЕуPЃЈ0ЃЌmЃЉдкyжсЩЯдЫЖЏЃЌЕБ![]() ЕФжЕзюДѓЪБЃЌЧѓЕуPЕФзјБъЃЎ
ЕФжЕзюДѓЪБЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЂйЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌЙ§
ЃЌЙ§![]() ЩЯвЛЕу
ЩЯвЛЕу![]() зї
зї![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌвд
ЃЌвд![]() ЮЊЖЅЕуЃЌ
ЮЊЖЅЕуЃЌ![]() ЮЊвЛБпЃЌзї
ЮЊвЛБпЃЌзї![]() ЃЌСэвЛБп
ЃЌСэвЛБп![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ

ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЃЛ
ЮЊЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉЕБЕу![]() ЮЊ
ЮЊ![]() жаЕуЪБЃЌ
жаЕуЪБЃЌ![]() ЕФаЮзДЮЊ ЃЛ
ЕФаЮзДЮЊ ЃЛ
ЃЈ3ЃЉбгГЄЭМЂйжаЕФ![]() ЕНЕу
ЕНЕу![]() ЪЙ
ЪЙ![]() СЌНг
СЌНг![]() ЕУЕНЭМЂкЃЌШє
ЕУЕНЭМЂкЃЌШє![]() ХаЖЯЫФБпаЮ
ХаЖЯЫФБпаЮ![]() ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ
ЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com