
����������10�֣�
�����������ѧϰ��������ȫ�ȵ��ж�����������SAS������ASA������AAS������SSS������ֱ��������ȫ�ȵ��ж�����������HL���������Ǽ����ԡ������������������ߺ�����һ�ߵĶԽǶ�Ӧ��ȡ������ν����о���
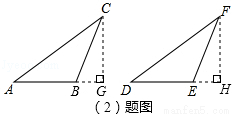
������˼�������Dz����������÷������Ա�ʾΪ���ڡ�ABC�͡�DEF�У�AC=DF��BC=EF����B=��E��Ȼ�ԡ�B���з��࣬�ɷ�Ϊ����B��ֱ�ǡ��۽ǡ���ǡ������������̽����
������̽����
��һ�����������B��ֱ��ʱ����ABC�ա�DEF��
��1����ͼ�٣��ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E=90�㣬���� ������֪��Rt��ABC��Rt��DEF��
�ڶ������������B�Ƕ۽�ʱ����ABC�ա�DEF��
��2����ͼ�ڣ��ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E���ҡ�B����E���Ƕ۽ǣ���֤����ABC�ա�DEF��
���������������B�����ʱ����ABC�͡�DEF��һ��ȫ�ȣ�
��3���ڡ�ABC�͡�DEF��AC=DF��BC=EF����B=��E���ҡ�B����E������ǣ������ó߹���ͼ����������DEF��ʹ��DEF�͡�ABC��ȫ�ȣ�����д������������ͼ�ۼ���
��4����B��Ҫ����ʲô�������Ϳ���ʹ��ABC�ա�DEF����ֱ��д�����ۣ��ڡ�ABC�͡�DEF�У�AC=DF��BC=EF����B=��E���ҡ�B����E������ǣ��� �����ABC�ա�DEF��


��1��HL����2��֤���������������3����ͼ�������������4����B�ݡ�A��
��������
�����������1������ֱ��������ȫ�ȵķ�����HL��֤����
��2������C��CG��AB��AB���ӳ�����G������F��FH��DE��DE���ӳ�����H�����ݵȽǵIJ�����������CBG=��FEH�������á��ǽDZߡ�֤����CBG�͡�FEHȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�CG=FH�������á�HL��֤��Rt��ACG��Rt��DFHȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵá�A=��D��Ȼ�����á��ǽDZߡ�֤����ABC�͡�DEFȫ�ȣ�
��3���Ե�CΪԲ�ģ���AC��Ϊ�뾶��������AB�ཻ�ڵ�D��E��B�غϣ�F��C�غϣ��õ���DEF���ABC��ȫ�ȣ�
��4����������������ۣ���B��С�ڡ�A���ɣ�
�����������1��HL��
��2����ͼ������C��CG��AB��AB���ӳ�����G������F��FH��DE��DE���ӳ�����H��
�ߡ�B=��E���ҡ�B����E���Ƕ۽ǣ���180�㩁��B=180�㩁��E������CBG=��FEH��
�ڡ�CBG�͡�FEH�У��ߡ�CBG=��FEH����G=��H=90�㣬BC=EF��
���CBG�ա�FEH��AAS������CG=FH��
��Rt��ACG��Rt��DFH����AC=DF��CG=FH����Rt��ACG��Rt��DFH��HL�������A=��D��
�ڡ�ABC�͡�DEF�У��ߡ�A=��D����ABC=��DEF��AC=DF�����ABC�ա�DEF��AAS����
��3����ͼ����DEF�͡�ABC��ȫ�ȣ�
��4������B�ݡ�A�����ABC�ա�DEF��
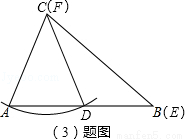
���㣺1��ȫ�������ε��ж������ʣ�2����ͼ��Ӧ���������ͼ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭���γǶ�̨�ն�˫��ѧУ�����ϵ�һ�μ�����ѧ���������棩 ���ͣ������
����ͼ��A��B��������ˮ�أ����ں���a��ͬ�࣬Ϊ�˷��������Ҫ�ںӱ߽�һ����ˮվ�� ����ˮ�͵�A��B���أ��ʸ�վ���ںӱ�ʲô�ط�����ʹ����������̣����� ͼ��ȷ���õ㣨������ͼ�ۼ���
����ͼ��ij����������ѧM��N�������ཻ��Ĺ�·a��b���ּƻ���һ�����ʲֿ⣬ϣ���ֿ������ѧ�ľ�����ȣ���������·�ľ���Ҳ��ȡ�����ȷ���ֿ�Ӧ�ý���ʲôλ������������ͼ���л��������Ʒ�����


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭�����ݷ�����ѧ���꼶��ѧ�ڵ�һ���ʼ���ѧ�Ծ��������棩 ���ͣ�ѡ����
�ڡ�ABC��һ��P����PA=PB=PC�����Pһ���ǡ�ABC�� ��
A��������ƽ���ߵĽ���
B�����ߴ�ֱƽ���ߵĽ���
C�������ߵĽ���
D���������ߵĽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭�ն�̨�ն�˫��ѧУ���꼶��ѧ�ڵ�һ���ʼ���ѧ���������棩 ���ͣ������
���ˮλ����1.2��,��Ϊ+1.2��,��ôˮλ�½�0.8��,��Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�꽭�ն�̨�ն�˫��ѧУ���꼶��ѧ�ڵ�һ���ʼ���ѧ���������棩 ���ͣ�ѡ����
�ѣ�+5��-��+3��-��-1��+��-5��д��ʡ�����ŵĺ͵���ʽ�� �� ��
A.-5-3+1-5 B.5-3-1-5
C.5+3+1-5 D.5-3+1-5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�������������������а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
����������8�֣���ͼ����Rt��ABC�У�AB=9��BC=6����B=90�㣬����ABC�۵���ʹA����BC���е�D�غϣ��ۺ�ΪMN�����߶�BN�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ�������������������а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��ͼ����ABC�У�AB=AC=10��BC=8��ADƽ�֡�BAC��BC�ڵ�D����EΪAC���е㣬����DE�����CDE���ܳ�Ϊ ��
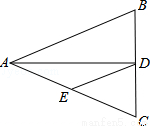
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ����������о��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ������
��10�֣���֪Rt��ABC����A=900������һ��Բ��ʹԲ��O��AC�ϣ�����AB��BC���ڵ�ֱ�����У���д������������ͼ�ۼ�����˵����ͼ�����ɣ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2014-2015ѧ��㶫ʡ��ͷ�а��꼶��ѧ�����п�����ѧ�Ծ��������棩 ���ͣ�ѡ����
��ͼ��ֱ��AB��CD�ཻ�ڵ�O��PE��CD��E��PF��AB��F����PE=PF����AOC=50�㣬���EOP�Ķ���Ϊ�� ��

A. 65�� B. 60�� C. 40�� D. 30��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com