
ΓΨΧβΡΩΓΩΡ≥–ΘΈΣΝΥΝΥΫβ―ß…ζΒΡΟΩ÷ήΩΈΆβ‘ΡΕΝ ±Φδ(”Ο![]() ±μ ΨΘ§ΒΞΈΜΘΚ–Γ ±)Θ§≤…»ΓΥφΜζ≥ι―υΒΡΖΫΖ®Ϋχ––Έ ΨμΒς≤ιΘ§Βς≤ιΫαΙϊΑ¥
±μ ΨΘ§ΒΞΈΜΘΚ–Γ ±)Θ§≤…»ΓΥφΜζ≥ι―υΒΡΖΫΖ®Ϋχ––Έ ΨμΒς≤ιΘ§Βς≤ιΫαΙϊΑ¥![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() Ζ÷ΈΣΥΡΗωΒ»ΦΕΘ§≤Δ“ά¥Έ”Ο
Ζ÷ΈΣΥΡΗωΒ»ΦΕΘ§≤Δ“ά¥Έ”Ο![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ΓΔ
ΓΔ![]() ±μ ΨΘ§ΗυΨίΒς≤ιΫαΙϊΘ§Μφ÷Τ≥…ΝΥ»γΆΦΥυ ΨΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦ.
±μ ΨΘ§ΗυΨίΒς≤ιΫαΙϊΘ§Μφ÷Τ≥…ΝΥ»γΆΦΥυ ΨΒΡΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦ.
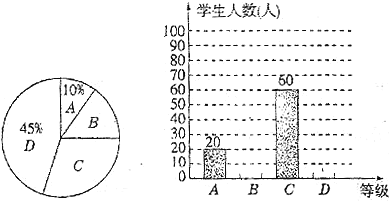
(1)Β»ΦΕ![]() ΒΡ―ß…ζ’ΦΒς≤ι―ß…ζΒΡΑΌΖ÷±» «Εύ…ΌΘΩ
ΒΡ―ß…ζ’ΦΒς≤ι―ß…ζΒΡΑΌΖ÷±» «Εύ…ΌΘΩ
(2)Β»ΦΕΈΣ![]() ΚΆ
ΚΆ![]() ΒΡ―ß…ζΖ÷±π”–Εύ…Ό»ΥΘΩ≤ΔΑ―Χθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
ΒΡ―ß…ζΖ÷±π”–Εύ…Ό»ΥΘΩ≤ΔΑ―Χθ–ΈΆ≥ΦΤΆΦ≤Ι≥δΆξ’ϊΘΜ
(3)»τΗΟ–Θ―ß…ζΙ≤”–![]() »ΥΘ§ΙάΦΤΟΩ÷ήΩΈΆβ‘ΡΕΝ ±ΦδΈΣ
»ΥΘ§ΙάΦΤΟΩ÷ήΩΈΆβ‘ΡΕΝ ±ΦδΈΣ![]() ΒΡ»Υ ΐ.
ΒΡ»Υ ΐ.
ΓΨ¥πΑΗΓΩ(1)30%ΘΜ(2)Β»ΦΕΈΣ![]() ―ß…ζ”–
―ß…ζ”–![]() »ΥΘ§Β»ΦΕΈΣ
»ΥΘ§Β»ΦΕΈΣ![]() ΒΡ―ß…ζ”–
ΒΡ―ß…ζ”–![]() »ΥΘΜ≤ΙΆΦΦϊΫβΈωΘΜ(3)180»Υ.
»ΥΘΜ≤ΙΆΦΦϊΫβΈωΘΜ(3)180»Υ.
ΓΨΫβΈωΓΩ
![]() ”…Χθ–ΈΆΦΓΔ…»–ΈΆΦ÷–Ηχ≥ωΒΡΦΕ±πAΒΡ ΐΉ÷Θ§Ω…ΦΤΥψ≥ωΒς≤ι―ß…ζ»Υ ΐΘ§”ΟCΒ»ΦΕ»Υ ΐ≥ΐ“‘Ήή»Υ ΐΩ…ΒΟCΒΡΑΌΖ÷±»ΘΜ
”…Χθ–ΈΆΦΓΔ…»–ΈΆΦ÷–Ηχ≥ωΒΡΦΕ±πAΒΡ ΐΉ÷Θ§Ω…ΦΤΥψ≥ωΒς≤ι―ß…ζ»Υ ΐΘ§”ΟCΒ»ΦΕ»Υ ΐ≥ΐ“‘Ήή»Υ ΐΩ…ΒΟCΒΡΑΌΖ÷±»ΘΜ![]() ”Ο
”Ο![]() ‘Ύ…»–ΈΆΦ÷–ΒΡΑΌΖ÷±»
‘Ύ…»–ΈΆΦ÷–ΒΡΑΌΖ÷±»![]() Ω…ΦΤΥψ≥ωB‘Ύ…»–ΈΆΦ÷–ΒΡΑΌΖ÷±»Θ§≥Υ“‘Ήή»Υ ΐΩ…ΒΟBΒΡ»Υ ΐΘ§‘Ό“άΨίΗςΒ»ΦΕ»Υ ΐ÷°ΚΆΒ»”ΎΉή»Υ ΐΩ…ΒΟCΒΡ»Υ ΐΘΜ
Ω…ΦΤΥψ≥ωB‘Ύ…»–ΈΆΦ÷–ΒΡΑΌΖ÷±»Θ§≥Υ“‘Ήή»Υ ΐΩ…ΒΟBΒΡ»Υ ΐΘ§‘Ό“άΨίΗςΒ»ΦΕ»Υ ΐ÷°ΚΆΒ»”ΎΉή»Υ ΐΩ…ΒΟCΒΡ»Υ ΐΘΜ![]() Ήή»Υ ΐ
Ήή»Υ ΐ![]() ΩΈΆβ‘ΡΕΝ ±Φδ¬ζΉψ
ΩΈΆβ‘ΡΕΝ ±Φδ¬ζΉψ![]() ΒΡΑΌΖ÷±»Φ¥ΒΟΥυ«σΘ°
ΒΡΑΌΖ÷±»Φ¥ΒΟΥυ«σΘ°
ΫβΘΚ![]() ±Ψ¥ΈΒς≤ιΒΡ―ß…ζ»Υ ΐΈΣ
±Ψ¥ΈΒς≤ιΒΡ―ß…ζ»Υ ΐΈΣ![]() »Υ
»Υ![]()
Υυ“‘CΦΕΥυ’ΦΒΡΑΌΖ÷±»ΈΣ![]() ΘΜ
ΘΜ![]() ΦΕΥυ’ΦΒΡΑΌΖ÷±»ΈΣΘΚ
ΦΕΥυ’ΦΒΡΑΌΖ÷±»ΈΣΘΚ![]() Θ§
Θ§
BΦΕΒΡ»Υ ΐΈΣ![]() »Υ
»Υ![]()
DΦΕΒΡ»Υ ΐΈΣΘΚ![]() »Υ
»Υ![]() Θ§
Θ§
≤Ι»ΪΆΦ–Έ»γœ¬ΘΚ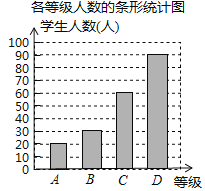
![]() ΙάΦΤΟΩ÷ήΩΈΆβ‘ΡΕΝ ±ΦδΈΣ
ΙάΦΤΟΩ÷ήΩΈΆβ‘ΡΕΝ ±ΦδΈΣ![]() ΒΡ»Υ ΐΈΣ
ΒΡ»Υ ΐΈΣ![]() »Υ
»Υ![]() Θ°
Θ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΈΣΝΥΫβ―ß…ζΕ‘άΚ«ρΓΔ”πΟΪ«ρΓΔΤΙ≈“«ρΓΔΧΏκΠΉ”ΓΔΧχ…ΰΒ»5œνΧε”ΐΜνΕ·ΒΡœ≤ΜΕ≥ΧΕ»Θ§Ρ≥–ΘΥφΜζ≥ι≤ι≤ΩΖ÷―ß…ζΘ§Ε‘ΥϊΟ«Ήνœ≤ΜΕΒΡΧε”ΐœνΡΩΘ®ΟΩ»Υ÷Μ―Γ“ΜœνΘ©Ϋχ––ΝΥΈ ΨμΒς≤ιΘ§≤ΔΫΪΆ≥ΦΤ ΐΨίΜφ÷Τ≥…»γœ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦΘΚ
«κΫβ¥πœ¬Ν–Έ ΧβΘΚ
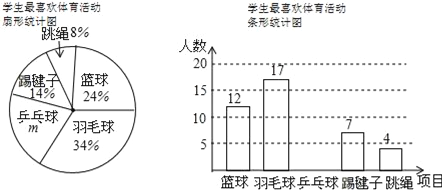
Θ®1Θ©m=ΓΓΓΓ%Θ§’β¥ΈΙ≤≥ι»ΓΝΥΓΓΓΓΟϊ―ß…ζΫχ––Βς≤ιΘΜ«κ≤Ι»ΪΧθ–ΈΆ≥ΦΤΆΦΘΜ
Θ®2Θ©»τ»Ϊ–Θ”–800Οϊ―ß…ζΘ§‘ρΗΟ–Θ‘Φ”–Εύ…ΌΟϊ―ß…ζœ≤Α°¥ράΚ«ρΘΩ
Θ®3Θ©―ß–ΘΉΦ±Η¥”œ≤ΜΕΧχ…ΰΜνΕ·ΒΡ4»ΥΘ®ΕΰΡ–Εΰ≈°Θ©÷–ΥφΜζ―Γ»Γ2»ΥΫχ––ΧεΡή≤β ‘Θ§«σ≥ιΒΫ“ΜΡ–“Μ≈°―ß…ζΒΡΗ≈¬ «Εύ…ΌΘΩ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷ΣΘΚ»γΆΦΘ§Ζ¥±»άΐΚ· ΐy= ![]() ΒΡΆΦœσ”κ“Μ¥ΈΚ· ΐy=x+bΒΡΆΦœσΫΜ
ΒΡΆΦœσ”κ“Μ¥ΈΚ· ΐy=x+bΒΡΆΦœσΫΜ
”ΎΒψAΘ®1Θ§4Θ©ΓΔΒψBΘ®-4Θ§nΘ©Θ°

Θ®1Θ©«σ“Μ¥ΈΚ· ΐΚΆΖ¥±»άΐΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©«σΓςOABΒΡΟφΜΐΘΜ
Θ®3Θ©÷±Ϋ”–¥≥ω“Μ¥ΈΚ· ΐ÷Β¥σ”ΎΖ¥±»άΐΚ· ΐ÷ΒΒΡΉ‘±δΝΩxΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
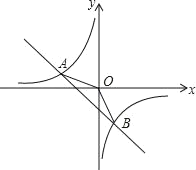
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§“Μ¥ΈΚ· ΐy1ΘΫax+bΘ®aΘ§bΈΣ≥Θ ΐΘ§«“aΓΌ0Θ©”κΖ¥±»άΐΚ· ΐy2ΘΫ![]() Θ®mΈΣ≥Θ ΐΘ§«“mΓΌ0Θ©ΒΡΆΦœσΫΜ”ΎΒψAΘ®©¹4Θ§2Θ©Θ§BΘ®2Θ§nΘ©Θ°
Θ®mΈΣ≥Θ ΐΘ§«“mΓΌ0Θ©ΒΡΆΦœσΫΜ”ΎΒψAΘ®©¹4Θ§2Θ©Θ§BΘ®2Θ§nΘ©Θ°
Θ®1Θ©«σΖ¥±»άΐΚ· ΐΚΆ“Μ¥ΈΚ· ΐΒΡΫβΈω ΫΘ°
Θ®2Θ©Ν§Ϋ”OAΘ§OBΘ§«σΓςAOBΒΡΟφΜΐΘ°
Θ®3Θ©÷±Ϋ”–¥≥ωΒ±0ΘΦy1ΘΦy2 ±Θ§Ή‘±δΝΩxΒΡ»Γ÷ΒΖΕΈßΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
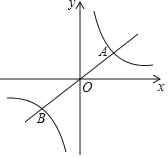
ΓΨΧβΡΩΓΩ»γΆΦΘ§Ζ¥±»άΐΚ· ΐyΘΫ![]() (kΘΨ0)ΒΡΆΦœσ”κ“Μ¥ΈΚ· ΐyΘΫ
(kΘΨ0)ΒΡΆΦœσ”κ“Μ¥ΈΚ· ΐyΘΫ![]() xΒΡΆΦœσΫΜ”ΎAΓΔBΝΫΒψ(ΒψA‘ΎΒΎ“Μœσœό)Θ°»τΒψAΒΡΚαΉχ±ξΈΣ4Θ°
xΒΡΆΦœσΫΜ”ΎAΓΔBΝΫΒψ(ΒψA‘ΎΒΎ“Μœσœό)Θ°»τΒψAΒΡΚαΉχ±ξΈΣ4Θ°
(1)«σkΒΡ÷ΒΘ°
(2)ΗυΨίΆΦœσΘ§÷±Ϋ”–¥≥ωΒ±![]() ΘΨ
ΘΨ![]() x ±Θ§xΒΡ»Γ÷ΒΖΕΈß.
x ±Θ§xΒΡ»Γ÷ΒΖΕΈß.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
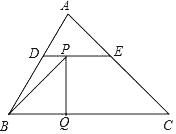
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓςABC÷–Θ§ΓœABCΘΫ60ΓψΘ§ΓœCΘΫ45ΓψΘ§ΒψDΘ§EΖ÷±πΈΣ±ΏABΘ§AC…œΒΡΒψΘ§«“DEΓΈBCΘ§BDΘΫDEΘΫ2Θ§CEΘΫ![]() Θ§BCΘΫ
Θ§BCΘΫ![]() Θ°Ε·ΒψP¥”ΒψB≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―ΊBΓζDΓζEΓζC‘»ΥΌ‘ΥΕ·Θ§‘ΥΕ·ΒΫΒψC ±ΆΘ÷ΙΘ°ΙΐΒψPΉςPQΓΆBC”ΎΒψQΘ§…ηΓςBPQΒΡΟφΜΐΈΣSΘ§ΒψPΒΡ‘ΥΕ· ±ΦδΈΣtΘ§‘ρSΙΊ”ΎtΒΡΚ· ΐΆΦœσ¥σ÷¬ΈΣΘ®ΓΓΓΓΘ©
Θ°Ε·ΒψP¥”ΒψB≥ωΖΔΘ§“‘ΟΩΟκ1ΗωΒΞΈΜ≥ΛΕ»ΒΡΥΌΕ»―ΊBΓζDΓζEΓζC‘»ΥΌ‘ΥΕ·Θ§‘ΥΕ·ΒΫΒψC ±ΆΘ÷ΙΘ°ΙΐΒψPΉςPQΓΆBC”ΎΒψQΘ§…ηΓςBPQΒΡΟφΜΐΈΣSΘ§ΒψPΒΡ‘ΥΕ· ±ΦδΈΣtΘ§‘ρSΙΊ”ΎtΒΡΚ· ΐΆΦœσ¥σ÷¬ΈΣΘ®ΓΓΓΓΘ©
A. 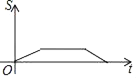 B.
B. 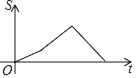
C. 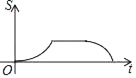 D.
D. 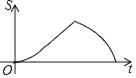
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§≈ΉΈοœΏy=ax2+bx+3ΫΜx÷α”ΎΒψAΘ®©¹1Θ§0Θ©ΚΆΒψBΘ®3Θ§0Θ©Θ°
Θ®1Θ©«σΗΟ≈ΉΈοœΏΥυΕ‘”ΠΒΡΚ· ΐΫβΈω ΫΘΜ
Θ®2Θ©»γΆΦ2Θ§ΗΟ≈ΉΈοœΏ”κy÷αΫΜ”ΎΒψCΘ§ΕΞΒψΈΣFΘ§ΒψDΘ®2Θ§3Θ©‘ΎΗΟ≈ΉΈοœΏ…œΘ°
ΔΌ«σΥΡ±Ώ–ΈACFDΒΡΟφΜΐΘΜ
ΔΎΒψP «œΏΕΈAB…œΒΡΕ·ΒψΘ®ΒψP≤Μ”κΒψAΓΔB÷ΊΚœΘ©Θ§ΙΐΒψPΉςPQΓΆx÷αΫΜΗΟ≈ΉΈοœΏ”ΎΒψQΘ§Ν§Ϋ”AQΓΔDQΘ§Β±ΓςAQD «÷±Ϋ«»ΐΫ«–Έ ±Θ§«σ≥ωΥυ”–¬ζΉψΧθΦΰΒΡΒψQΒΡΉχ±ξΘ°
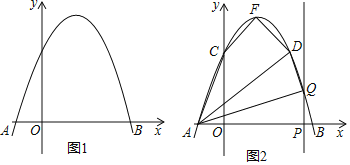
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§≈ΉΈοœΏy1=![]() Θ®x+1Θ©2+1”κy2=aΘ®x©¹4Θ©2©¹3ΫΜ”ΎΒψAΘ®1Θ§3Θ©Θ§ΙΐΒψAΉςx÷αΒΡΤΫ––œΏΘ§Ζ÷±πΫΜΝΫΧθ≈ΉΈοœΏ”ΎBΓΔCΝΫΒψΘ§«“DΓΔEΖ÷±πΈΣΕΞΒψΘ°‘ρœ¬Ν–Ϋα¬έΘΚΔΌa=
Θ®x+1Θ©2+1”κy2=aΘ®x©¹4Θ©2©¹3ΫΜ”ΎΒψAΘ®1Θ§3Θ©Θ§ΙΐΒψAΉςx÷αΒΡΤΫ––œΏΘ§Ζ÷±πΫΜΝΫΧθ≈ΉΈοœΏ”ΎBΓΔCΝΫΒψΘ§«“DΓΔEΖ÷±πΈΣΕΞΒψΘ°‘ρœ¬Ν–Ϋα¬έΘΚΔΌa=![]() ΘΜΔΎAC=AEΘΜΔέΓςABD «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΜΔήΒ±xΘΨ1 ±Θ§y1ΘΨy2ΓΓ Τδ÷–’ΐ»ΖΫα¬έΒΡΗω ΐ «Θ® )
ΘΜΔΎAC=AEΘΜΔέΓςABD «Β»―ϋ÷±Ϋ«»ΐΫ«–ΈΘΜΔήΒ±xΘΨ1 ±Θ§y1ΘΨy2ΓΓ Τδ÷–’ΐ»ΖΫα¬έΒΡΗω ΐ «Θ® )

A. 1ΗωBΘ°2ΗωCΘ°3ΗωDΘ°4Ηω
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏy=ax2+bx+cΘ®aΓΌ0Θ©Ψ≠ΙΐΒψAΘ®3Θ§0Θ©Θ§BΘ®©¹1Θ§0Θ©Θ§CΘ®0Θ§©¹3Θ©Θ°
Θ®1Θ©«σΗΟ≈ΉΈοœΏΒΡΫβΈω ΫΘΜ
Θ®2Θ©»τ“‘ΒψAΈΣ‘≤–ΡΒΡ‘≤”κ÷±œΏBCœύ«–”ΎΒψMΘ§«σ«–ΒψMΒΡΉχ±ξΘΜ
Θ®3Θ©»τΒψQ‘Ύx÷α…œΘ§ΒψP‘Ύ≈ΉΈοœΏ…œΘ§ «Ζώ¥φ‘Ύ“‘ΒψBΘ§CΘ§QΘ§PΈΣΕΞΒψΒΡΥΡ±Ώ–Έ «ΤΫ––ΥΡ±Ώ–ΈΘΩ»τ¥φ‘ΎΘ§«σΒψPΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com