
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴的负半轴,点
轴的负半轴,点![]() 在
在![]() 轴的正半轴,与
轴的正半轴,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() ,
,![]() .则下列判断中正确的是( )
.则下列判断中正确的是( )
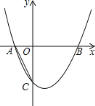
A. 此抛物线的解析式为![]()
B. 当![]() 时,
时,![]() 随着
随着![]() 的增大而增大
的增大而增大
C. 此抛物线与直线![]() 只有一个交点
只有一个交点
D. 在此抛物线上的某点![]() ,使
,使![]() 的面积等于
的面积等于![]() ,这样的点共有三个
,这样的点共有三个
【答案】C
【解析】
利用CO=2AO,而CO=BO,AB=3,可得出AO=1,BO=OC=2,即可求出二次函数的解析式,由二次函数的对称轴,可得出当x>0时,y随着x的增大而先减小再增大,由二次函数的最小值为-![]() ,可得此抛物线与直线y=-
,可得此抛物线与直线y=-![]() 只有一个交点,由△MAB的面积等于4,得出M到x轴的距离为
只有一个交点,由△MAB的面积等于4,得出M到x轴的距离为![]() ,这样的点共有2个.即可选出答案.
,这样的点共有2个.即可选出答案.
解:∵CO=2AO,而CO=BO,AB=3,
∴AO=1,BO=OC=2,即A(-1,0),B(2,0),C(0,-2),
∴二次函数的解析式为y=x2-x-2,故A错误.
∵二次函数的对称轴为x=![]() ,
,
∴当x>0时,y随着x的增大而先减小再增大,故B错误.
∵此二次函数的最小值为-![]() ,
,
∴此抛物线与直线y=-![]() 只有一个交点,C正确.
只有一个交点,C正确.
∵要使△MAB的面积等于4,须使M到x轴的距离为![]() ,这样的点共有2个,故B错误.
,这样的点共有2个,故B错误.
故选:C.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=6,AC=BC=5,将△ABC折叠,使点A落在BC边上的点D处,折痕为EF(点E.F分别在边AB、AC上).当以B.E.D为顶点的三角形与△DEF相似时,BE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师用![]() 个
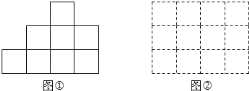
个![]() 的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边
的小正立方体摆出一个立体图形,它的正视图如图①所示,且图中任两相邻的小正立方体至少有一棱边![]() 共享,或有一面
共享,或有一面![]() 共享.老师拿出一张
共享.老师拿出一张![]() 的方格纸(如图②),请小荣将此
的方格纸(如图②),请小荣将此![]() 个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有________种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
个小正立方体依正视图摆放在方格纸中的方格内,请问小荣摆放完后的左视图有________种.(小正立方体摆放时不得悬空,每一小正立方体的棱边与水平线垂直或平行)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销的一种进价为每件![]() 元的运动休闲杉热销.据市场调查分析,若每件按
元的运动休闲杉热销.据市场调查分析,若每件按![]() 元销售出
元销售出![]() 件;销售单价每涨价
件;销售单价每涨价![]() 元,月销售量就减少
元,月销售量就减少![]() 件.针对这种运动休闲杉的销售情况,请解答以下问题:
件.针对这种运动休闲杉的销售情况,请解答以下问题:
![]() 设销售单价为每件
设销售单价为每件![]() 元,月销售利润为
元,月销售利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式(不必写出
之间的函数关系式(不必写出![]() 的取值范围);
的取值范围);
![]() 商店想使月销售利润达到
商店想使月销售利润达到![]() 元,并使销售量尽量大,请问该休闲杉的销售单价应定为多少元?
元,并使销售量尽量大,请问该休闲杉的销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中, AB =AC=24 cm, BC=16cm,AD= BD.如果点P在线段BC上以 2 cm/s 的速度由B点向C点运动,同时,点 Q在线段CA上以v cm/s 的速度由C点向A点运动,那么当△BPD 与△CQP全等时,v =( )
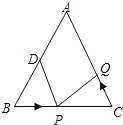
A.3B.4C.2或 4D.2或3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年4月23日是 “世界读书日”,宜宾市某中学举行“多读书,读好书”活动,对学生的课外读书时间进行了随机问卷调查,用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题:
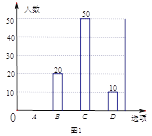
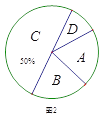
(1)本次接受问卷调查的学生共有________人,在扇形统计图中“D”选项所占的百分比为________;
(2)扇形统计图中,“B”选项所对应扇形圆心角为________度;
(3)请补全条形统计图;
(4)若该校共有1200名学生,则该校学生课外读书时间在“A”选项的约有_____人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com