
【题目】如图,在等腰![]() 中,
中,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交过点
,交过点![]() 直线
直线![]() 交于点
交于点![]() ,且
,且![]() ,
,![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() 时,则
时,则![]() ________.
________.

【答案】![]()
【解析】
作辅助线构建等腰直角三角形和直角三角形,分别得出△BDF和△AFM是等腰直角三角形,得BF=DB=1,AM=FM,根据sin∠ABC=![]() 设未知数,表示BM和AM的长,列方程得出各线段的长,并证出AG是△EFC的中位线,由此得出结论.
设未知数,表示BM和AM的长,列方程得出各线段的长,并证出AG是△EFC的中位线,由此得出结论.
过A作AM⊥BC,垂足为M,延长AD、CB交于F,取FC的中点G,连接AG,
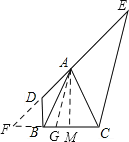
∵∠ADB=135°,
∴∠BDF=180°-135°=45°,
∴△BDF是等腰直角三角形,
∴BF=DB=1,
由勾股定理得:DF=![]() ,
,
在Rt△AFM中,∵∠F=45°,
∴AM=FM,
设AM=2![]() x,AB=5x,则BM=
x,AB=5x,则BM=![]() x,
x,
由AM=FM得:![]() x+1=2
x+1=2![]() x,
x,
x=![]() ,
,
∴BM=MC=![]() x=1,AM=2,
x=1,AM=2,
∵AM⊥BC,DB⊥BC,
∴DB∥AM,
∵FB=BM,
∴FD=AD,
∵AE=2AD,
∴AE=AF,
∴AG是△EFC的中位线,
∴EC=2AG,
∵MG=![]() ,
,
由勾股定理得:AG=![]() =
=![]() ,
,
∴EC=![]() .
.


 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE,垂足分别为点D,E.(1)求证:△ACD≌△CBE;(2)若BE=5,AD=12,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙二人做某种机械零件,已知每小时甲比乙少做8个,甲做120个所用的时间与乙做150个所用的时间相等.
(1)甲、乙二人每小时各做零件多少个?
(2)甲做几小时与乙做4小时所做机械零件数相等?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 在
在![]() 轴的负半轴,点
轴的负半轴,点![]() 在
在![]() 轴的正半轴,与
轴的正半轴,与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() ,
,![]() .则下列判断中正确的是( )
.则下列判断中正确的是( )
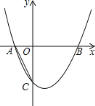
A. 此抛物线的解析式为![]()
B. 当![]() 时,
时,![]() 随着
随着![]() 的增大而增大
的增大而增大
C. 此抛物线与直线![]() 只有一个交点
只有一个交点
D. 在此抛物线上的某点![]() ,使
,使![]() 的面积等于
的面积等于![]() ,这样的点共有三个
,这样的点共有三个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() .
.![]() 、
、![]() 是边
是边![]() 、
、![]() 边上的动点,
边上的动点,![]() 从
从![]() 出发向
出发向![]() 运动,同时
运动,同时![]() 以相同的速度从
以相同的速度从![]() 出发向
出发向![]() 运动,
运动,![]() 运动到
运动到![]() 停止.
停止.![]() 为
为![]() 中点.
中点.
![]() 试探究
试探究![]() 的形状,并说明理由.
的形状,并说明理由.
![]() 在运动过程中,四边形
在运动过程中,四边形![]() 可能成为正方形吗?如能求正方形的边长.
可能成为正方形吗?如能求正方形的边长.
![]() 当
当![]() 为多少时,
为多少时,![]() 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元.
(1)求甲种树苗每棵多少元?
(2)若准备用3800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳市某学校抽样调查,A类学生骑共享单车,B类学生坐公交车、私家车等,C类学生步行,D类学生(其它),根据调查结果绘制了不完整的统计图.
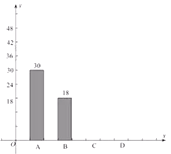
类型 | 频数 | 频率 |
A | 30 |
|
B | 18 | 0.15 |
C |
| 0.40 |
D |
|
|
(1)学生共________人, ![]() ________,
________, ![]() ________;
________;
(2)补全条形统计图;
(3)若该校共有2000人,骑共享单车的有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△![]() 在平面直角坐标系中的位置如图所示.
在平面直角坐标系中的位置如图所示.
(1)作出△![]() 关于
关于![]() 轴对称的△
轴对称的△![]() ,并写出△
,并写出△![]() 各顶点的坐标;
各顶点的坐标;
(2)将△![]() 向右平移6个单位,作出平移后的△
向右平移6个单位,作出平移后的△![]() ,并写出△
,并写出△![]() 各顶点的坐标;
各顶点的坐标;
(3)观察△![]() 和△
和△![]() ,它们是否关于某直线对称?若是,请用粗线条画出对称轴.
,它们是否关于某直线对称?若是,请用粗线条画出对称轴.
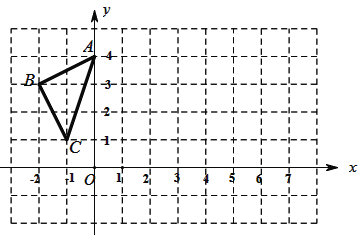
查看答案和解析>>
科目:初中数学 来源: 题型:
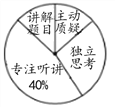
【题目】某地区教育部门为了解初中数学课堂中学生参与情况,并按“主动质疑、独立思考、专注听讲、讲解题目”四个项目进行评价.检测小组随机抽查部分学校若干名学生,并将抽查学生的课堂参与情况绘制成如图所示的扇形统计图和条形统计图(均不完整).请根据统计图中的信息解答下列问题:
(1)本次抽查的样本容量是 ;
(2)在扇形统计图中,“主动质疑”对应的圆心角为 度;
(3)将条形统计图补充完整;
(4)如果该地区初中学生共有60000名,那么在课堂中能“独立思考”的学生约有多少人?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com