
����Ŀ��ij�̵꾭����һ�ֽ���Ϊÿ��![]() Ԫ���˶�����ɼ���������г������������ÿ����
Ԫ���˶�����ɼ���������г������������ÿ����![]() Ԫ���۳�
Ԫ���۳�![]() �������۵���ÿ�Ǽ�
�������۵���ÿ�Ǽ�![]() Ԫ�����������ͼ���
Ԫ�����������ͼ���![]() ������������˶�����ɼ����������������������⣺
������������˶�����ɼ����������������������⣺
![]() �����۵���Ϊÿ��
�����۵���Ϊÿ��![]() Ԫ������������Ϊ
Ԫ������������Ϊ![]() Ԫ����
Ԫ����![]() ��
��![]() ֮��ĺ�����ϵʽ������д��
֮��ĺ�����ϵʽ������д��![]() ��ȡֵ��Χ����
��ȡֵ��Χ����
![]() �̵���ʹ����������ﵽ
�̵���ʹ����������ﵽ![]() Ԫ����ʹ���������������ʸ�����ɼ�����۵���Ӧ��Ϊ����Ԫ��
Ԫ����ʹ���������������ʸ�����ɼ�����۵���Ӧ��Ϊ����Ԫ��
���𰸡���1��y=-10x2+1400x-40000����2�����۵���Ӧ��Ϊ![]() Ԫ��
Ԫ��
��������
��1�����ݡ����۵���ÿ��1Ԫ�����������ͼ���10��������֪����������=500-�����۵���-50����10��Ȼ���������������=ÿ������������۵������������y��x֮��ĺ�����ϵʽ��
��2����y=8000���루1��������ĺ�����ϵʽ���õ�����x�ķ��̣��ⷽ�̼���.
�⣺��1�������۵��۶�Ϊÿǧ��xԪʱ����������Ϊ��[500-��x-50����10]����
ÿ�������������ǣ���x-40��Ԫ��
����������������y=��x-40��[500-��x-50����10]=��x-40����1000-10x��=-10x2+1400x-40000��
��y��x�ĺ�������ʽΪ��y=-10x2+1400x-40000��
��2���������-10x2+1400x-40000=8000��
���x1=60��x2=80��
��ΪҪʹʹ����������������ֻ��ȡx=60��
�����۵���Ӧ��Ϊ60Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��������OAB�У���AOB=110�㣬�뾶OA=18��������OAB�ع���B��ֱ���۵�����Oǡ�����ڻ�AB�ϵĵ�D�����ۺ۽�OA�ڵ�C����AD�ij�Ϊ��������
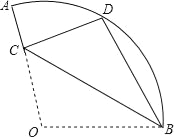
A. 2�� B. 3�� C. 4�� D. 5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
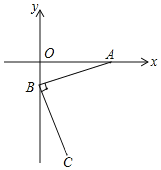
����Ŀ����ͼ����֪A��3��0����B��0����1��������AB������B�Ĵ���BC��ʹBC��BA�����C������_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���![]() ��ͼ����ͼ��ʾ���Գ�����ֱ��
��ͼ����ͼ��ʾ���Գ�����ֱ��![]() �������½��ۣ���
�������½��ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ��������ȷ�Ľ��۵ĸ�����( )
��������ȷ�Ľ��۵ĸ�����( )
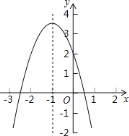
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������![]() ��
��![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() ��
��![]() ��ĸ����ᣬ��
��ĸ����ᣬ��![]() ��
��![]() ��������ᣬ��
��������ᣬ��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ��
��![]() ��
��![]() ���������ж�����ȷ����( )
���������ж�����ȷ����( )
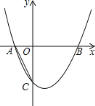
A. �������ߵĽ���ʽΪ![]()
B. ��![]() ʱ��
ʱ��![]() ����
����![]() �����������
�����������
C. ����������ֱ��![]() ֻ��һ������
ֻ��һ������
D. �ڴ��������ϵ�ij��![]() ��ʹ
��ʹ![]() ���������
���������![]() �������ĵ㹲������
�������ĵ㹲������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���D��m��m+8���ڵڶ����ޣ���B��0��n����y���������ϣ���DA��x�ᣬ����ΪA����֪OA��OB��ֵ��2���ı���AOBD�����Ϊ12��

��1����m��n��ֵ��
��2����ͼ2��CΪAO���е㣬DC��AB�ཻ�ڵ�E��AF��BD������ΪF����֤��AF��DE��
��3����ͼ3����G������AD�ϣ���GA��GB��HΪGB�ӳ�����һ�㣬����HAN��y���ڵ�N���ҡ�HAN����HBO����NB��HB��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019��3��12���ǵ�41��ֲ���ڣ�ij��λ������չֲ�������������ס����������磬��800Ԫ�����������Ŀ�������680Ԫ������������Ŀ�����ͬ����������ÿ�ñȼ�������ÿ����6Ԫ��
��1�����������ÿ�ö���Ԫ��
��2��������3800Ԫ����ס����������繲100�ã�������Ҫ��������������ٿã�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪A��3��m����B����2����3����ֱ��AB��ij������������ͼ����������㣮
��1����ֱ��AB�ͷ����������Ľ���ʽ��
��2���۲�ͼ��ֱ��д����x����ʲô��Χʱ��ֱ��AB��˫���ߵ��·���
��3��������������ͼ�����Ƿ���ڵ�C��ʹ����OBC�����������OAB���������������ڣ�˵�����ɣ�������ڣ�����������������е�C�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
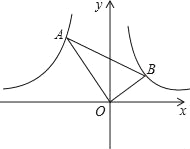
����Ŀ����ͼ����֪��A��B�ֱ��Ƿ���������y=![]() ��x��0����y=
��x��0����y=![]() ��x��0����ͼ���ϵĵ㣬�ҡ�AOB=90�㣬tan��BAO=
��x��0����ͼ���ϵĵ㣬�ҡ�AOB=90�㣬tan��BAO=![]() ����k��ֵΪ��������
����k��ֵΪ��������
A. 2 B. ��2 C. 4 D. ��4
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com