
【题目】如图,已知点A,B分别是反比例函数y=![]() (x<0),y=
(x<0),y=![]() (x>0)的图象上的点,且∠AOB=90°,tan∠BAO=
(x>0)的图象上的点,且∠AOB=90°,tan∠BAO=![]() ,则k的值为( )
,则k的值为( )
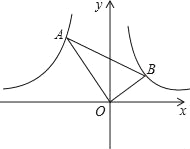
A. 2 B. ﹣2 C. 4 D. ﹣4
【答案】D
【解析】
首先过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,易得△OBD∽△AOC,又由点A,B分别在反比例函数y=![]() (x<0),y=
(x<0),y=![]() (x>0)的图象上,即可得S△OBD=
(x>0)的图象上,即可得S△OBD=![]() ,S△AOC=
,S△AOC=![]() |k|,然后根据相似三角形面积的比等于相似比的平方,即可求出k的值
|k|,然后根据相似三角形面积的比等于相似比的平方,即可求出k的值
解:过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
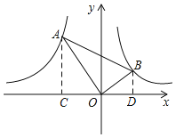
∴∠ACO=∠ODB=90°,
∴∠OBD+∠BOD=90°,
∵∠AOB=90°,
∴∠BOD+∠AOC=90°,
∴∠OBD=∠AOC,
∴△OBD∽△AOC,
又∵∠AOB=90°,tan∠BAO=![]() ,
,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,即
,即![]() ,
,
解得k=±4,
又∵k<0,
∴k=-4,
故选:D.


科目:初中数学 来源: 题型:
【题目】某商店经销的一种进价为每件![]() 元的运动休闲杉热销.据市场调查分析,若每件按
元的运动休闲杉热销.据市场调查分析,若每件按![]() 元销售出
元销售出![]() 件;销售单价每涨价
件;销售单价每涨价![]() 元,月销售量就减少
元,月销售量就减少![]() 件.针对这种运动休闲杉的销售情况,请解答以下问题:
件.针对这种运动休闲杉的销售情况,请解答以下问题:
![]() 设销售单价为每件
设销售单价为每件![]() 元,月销售利润为
元,月销售利润为![]() 元,求
元,求![]() 与
与![]() 之间的函数关系式(不必写出
之间的函数关系式(不必写出![]() 的取值范围);
的取值范围);
![]() 商店想使月销售利润达到
商店想使月销售利润达到![]() 元,并使销售量尽量大,请问该休闲杉的销售单价应定为多少元?
元,并使销售量尽量大,请问该休闲杉的销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:课堂上,同学们研究几何变量之间的函数关系问题:如图,菱形ABCD的对角线AC,BD相交于点O,AC=4,BD=2.点P是AC上的一个动点,过点P作MN⊥AC,垂足为点P(点M在边AD、DC上,点N在边AB、BC上).设AP的长为x(0≤x≤4),△AMN的面积为y.

建立模型:(1)y与x的函数关系式为:![]() ,
,
解决问题:(2)为进一步研究y随x变化的规律,小明想画出此函数的图象.请你补充列表,并在如图的坐标系中画出此函数的图象:
x | 0 |
| 1 |
| 2 |
| 3 |
| 4 |
y | 0 |
|
|
|
|
|
|
| 0 |
(3)观察所画的图象,写出该函数的两条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)是由抛物线y=﹣x2+x+2先作关于y轴的轴对称图形,再将所得到的图象向下平移3个单位长度得到的,点Q1(﹣2.25,q1),Q2(1.5,q2)都在抛物线y=ax2+bx+c(a≠0)上,则q1,q2的大小关系是( )
A. q1>q2 B. q1<q2 C. q1=q2 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年4月23日是 “世界读书日”,宜宾市某中学举行“多读书,读好书”活动,对学生的课外读书时间进行了随机问卷调查,用调查结果绘制了图1、图2两幅统计图(均不完整),请根据统计图解答以下问题:
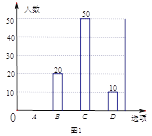
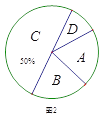
(1)本次接受问卷调查的学生共有________人,在扇形统计图中“D”选项所占的百分比为________;
(2)扇形统计图中,“B”选项所对应扇形圆心角为________度;
(3)请补全条形统计图;
(4)若该校共有1200名学生,则该校学生课外读书时间在“A”选项的约有_____人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,圆C过原点并与坐标轴分别交于A、D两点,已知点B为圆C圆周上一动点,且∠ABO=30°,点D的坐标为(0,2![]() ).
).
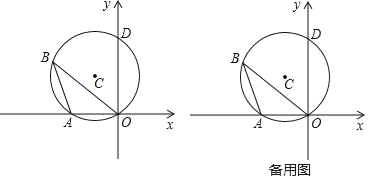
(1)直接写出圆心 C 的坐标;
(2)当△BOD为等边三角形时,求点B的坐标;
(3)若以点B为圆心、r为半径作圆B,当圆B与两个坐标轴同时相切时,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】泰勒斯是古希腊哲学家,相传他利用三角形全等的方法求出岸上一点到海中一艘船的距离.如图,B是观察点,船A在B的正前方,过B作AB的垂线,在垂线上截取任意长BD,C是BD的中点,观察者从点D沿垂直于BD的DE方向走,直到点E、船A和点C在一条直线上,那么△ABC≌△EDC,从而量出DE的距离即为船离岸的距离AB,这里判定△ABC≌△EDC的方法是( )

A.SASB.ASAC.AASD.SSS
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点B、C、D都在⊙O上,过C点作CA∥BD,交OD的延长线于点A,连接BC,∠B=∠A=30,BD=![]() 。
。
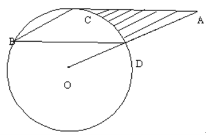
(1)求证:AC是⊙O的切线。
(2)求由线段AC、AD与弧CD所围成的阴影部分的面积(结果保留π)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知半径为2的⊙O与直线l相切于点A,点P是直径AB左侧半圆上的动点,过点P作直线l的垂线,垂足为C,PC与⊙O交于点D,连接PA、PB,设PC的长为x(2<x<4)
【1】当![]() 时,求弦PA、PB的长度;
时,求弦PA、PB的长度;
【2】当x为何值时,PD×CD的值最大?最大值是多少?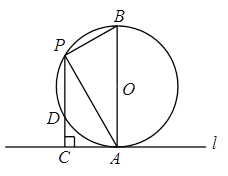
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com