
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У���D��m��m+8���ڵڶ����ޣ���B��0��n����y���������ϣ���DA��x�ᣬ����ΪA����֪OA��OB��ֵ��2���ı���AOBD�����Ϊ12��

��1����m��n��ֵ��
��2����ͼ2��CΪAO���е㣬DC��AB�ཻ�ڵ�E��AF��BD������ΪF����֤��AF��DE��
��3����ͼ3����G������AD�ϣ���GA��GB��HΪGB�ӳ�����һ�㣬����HAN��y���ڵ�N���ҡ�HAN����HBO����NB��HB��ֵ��
���𰸡���1��![]() ��2�������������3��NB��FB��4���Ƕ�ֵ����������H��GB���ӳ������˶�ʱ��NB��HB��ֵ���ᷢ���仯��
��2�������������3��NB��FB��4���Ƕ�ֵ����������H��GB���ӳ������˶�ʱ��NB��HB��ֵ���ᷢ���仯��
��������
��1���ɵ�D����B��������ı���AOBD�����Ϊ12�����з����飬�ⷽ���鼴�ɣ�
��2���ɣ�1����֪��AD��OA��4��OB��2���������AB��BD��![]() ������SAS��֤��DAC�ա�AOB�����ɵá�AEC��90�������������������ʽ������֤��
������SAS��֤��DAC�ա�AOB�����ɵá�AEC��90�������������������ʽ������֤��
��3��ȡOC��OB������AC�����ݶԳ��Կɵá�ABC����ACB��AB��AC��֤����ABH�ա�CAN�����ɵõ�����.
�⣺��1��������
���![]() ��
��
��2����ͼ2�У�

�ɣ�1����֪��A����4��0����B��0��2����D����4��4����
��AD��OA��4��OB��2��
���ɹ��ɶ����ɵã�AB��BD��![]() ��
��
��AC��OC��2��
��AC��OB��
�ߡ�DAC����AOB��90����AD��OA��
���DAC�ա�AOB��SAS����
���ADC����BAO��
�ߡ�ADC+��ACD��90����
���EAC+��ACE��90����
���AEC��90����
��AF��BD��DE��AB��
��S��ADB��![]() ABAE��
ABAE��![]() BDAF��
BDAF��
��AB��BD��
��DE��AF��
��3���⣺��ͼ��ȡOC��OB������AC�����ݶԳ��Կɵá�ABC����ACB��AB��AC��

��AG��BG��
���GAB����GBA��
��GΪ����AD�ϵ�һ�㣬
��AG��y�ᣬ
���GAB����ABC��
���ACB����EBA��
��180������GBA��180������ACB��
����ABG����ACN��
�ߡ�GAN����GBO��
���AGB����ANC��
����ABG����ACN��
 ��
��
���ABH�ա�ACN��AAS����
��BF��CN��
��NB��HB��NB��CN��BC��2OB��
��OB��2
��
������H��GB���ӳ������˶�ʱ��NB��HB��ֵ���ᷢ���仯��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ȱ�������ABC����DΪ�߶�BC��һ�㣬���߶�DBΪ�����Ҳ�����DEB��ʹDE��CD������ADB��m������BDE����180��2m���������DBE�Ķ����ǣ�������

A.��m��60����B.��180��2m����C.��2m��90����D.��120��m����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�D��BC���ϵ�һ�㣬AB��DB��BEƽ�֡�ABC����AC���ڵ�E������DE��

��1����֤��AE��DE��
��2������A��100������C��50�������AEB�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC�У�CDΪ��ABC�����ߣ���E��CD�ϣ��ҡ�AED����BCD��

��1����֤��AE��BC��
��2����ͼ2������BE����AB��AC��2DE����CBE��14�������ACD�Ķ���Ϊ�� ����ֱ��д���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵꾭����һ�ֽ���Ϊÿ��![]() Ԫ���˶�����ɼ���������г������������ÿ����
Ԫ���˶�����ɼ���������г������������ÿ����![]() Ԫ���۳�
Ԫ���۳�![]() �������۵���ÿ�Ǽ�
�������۵���ÿ�Ǽ�![]() Ԫ�����������ͼ���
Ԫ�����������ͼ���![]() ������������˶�����ɼ����������������������⣺
������������˶�����ɼ����������������������⣺
![]() �����۵���Ϊÿ��
�����۵���Ϊÿ��![]() Ԫ������������Ϊ
Ԫ������������Ϊ![]() Ԫ����
Ԫ����![]() ��
��![]() ֮��ĺ�����ϵʽ������д��
֮��ĺ�����ϵʽ������д��![]() ��ȡֵ��Χ����
��ȡֵ��Χ����
![]() �̵���ʹ����������ﵽ
�̵���ʹ����������ﵽ![]() Ԫ����ʹ���������������ʸ�����ɼ�����۵���Ӧ��Ϊ����Ԫ��
Ԫ����ʹ���������������ʸ�����ɼ�����۵���Ӧ��Ϊ����Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������һ����̫�����������ٵ����ӣ������ʱ¥����Ͳ��ܲɵ����⣬һ���ļ�����¥�����ܵ��������䣬���Զ�����ѡ����ʱȷ��������������ʱ�����⽭ij����С����һ����Ϊ���Ϸ���ľ���¥���þ���¥��һ¥�Ǹ�Ϊ![]() ��С�����У����������Ǿ���ס�����ּƻ��ڸ�¥ǰ��
��С�����У����������Ǿ���ס�����ּƻ��ڸ�¥ǰ��![]() �״���һ����¥����֪�⽭�������������������ˮƽ�нǴ�ԼΪ
�״���һ����¥����֪�⽭�������������������ˮƽ�нǴ�ԼΪ![]() �����ο�������
�����������![]() ��
��![]() ��
��
![]() ����ʱ����Ҫʹ�ó��вɹⲻ��Ӱ�죬����¥�ĸ߶Ȳ��ܳ��������ף����������������
����ʱ����Ҫʹ�ó��вɹⲻ��Ӱ�죬����¥�ĸ߶Ȳ��ܳ��������ף����������������
![]() ���½��Ĵ�¥��
���½��Ĵ�¥��![]() �ף�������ʱ���������ϵľ���ס���ɹ��Ƿ���Ӱ�죬Ϊʲô��
�ף�������ʱ���������ϵľ���ס���ɹ��Ƿ���Ӱ�죬Ϊʲô��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���y��kx��b�뷴��������y��![]() ��x��0������A��2��4����B��a��1������x�ᣬy��ֱ��ڵ�C��D��
��x��0������A��2��4����B��a��1������x�ᣬy��ֱ��ڵ�C��D��
��1��ֱ��д��һ�κ���y��kx��b�ı���ʽ�ͷ���������y��![]() ��x��0���ı���ʽ��
��x��0���ı���ʽ��
��2����֤��AD��BC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AE��BF��AE=BF��A��C��D��B��ͬһֱ���ϣ�Ҫʹ��ADE�ա�BCF�������ӵ�һ������������____________________��(дһ������).

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ԲC��ԭ�㲢��������ֱ���A��D���㣬��֪��BΪԲCԲ����һ���㣬�ҡ�ABO=30������D������Ϊ��0��2![]() ����
����
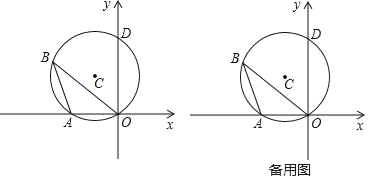
��1��ֱ��д��Բ�� C �����ꣻ
��2������BODΪ�ȱ�������ʱ�����B�����ꣻ
��3�����Ե�BΪԲ�ġ�rΪ�뾶��ԲB����ԲB������������ͬʱ����ʱ�����B�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com