
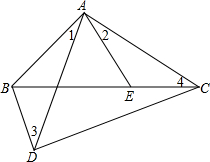
 如图,D是△ABC外一点,E是边BC上一点,∠1=∠2,∠3=∠4.图中有几对相似的三角形?(不准添加新的字母)请说明理由.
如图,D是△ABC外一点,E是边BC上一点,∠1=∠2,∠3=∠4.图中有几对相似的三角形?(不准添加新的字母)请说明理由. 分析 利用有两组角对应相等的两个三角形相似可得△ABD∽△AEC,根据相似三角形对应边成比例得出$\frac{AB}{AE}$=$\frac{AD}{AC}$,由比例的性质得到$\frac{AB}{AD}$=$\frac{AE}{AC}$,又由∠1=∠2得出∠BAE=∠DAC,根据两组对应边的比相等且夹角对应相等的两个三角形相似得出△ABE∽△ADC.
解答 解:不添加新的字母,图中有2对相似的三角形,△ABD∽△AEC,△ABE∽△ADC.理由如下:
在△ABD与△AEC中,
∵∠1=∠2,∠3=∠4,
∴△ABD∽△AEC,
∴$\frac{AB}{AE}$=$\frac{AD}{AC}$,
∴$\frac{AB}{AD}$=$\frac{AE}{AC}$,
∵∠1=∠2,
∴∠BAE=∠DAC.
在△ABE与△ADC中,
∵$\frac{AB}{AD}$=$\frac{AE}{AC}$,∠BAE=∠DAC,
∴△ABE∽△ADC.
点评 本题主要考查了相似三角形的判定,判定两个三角形相似的方法有:
(1)平行线法:平行于三角形的一边的直线与其他两边相交,所构成的三角形与原三角形相似;
(2)三边法:三组对应边的比相等的两个三角形相似;
(3)两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;
(4)两角法:有两组角对应相等的两个三角形相似.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:解答题
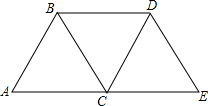 如图,把△ABC按AC方向平移,平移的距离是AC的长度,则平移后点B平移到点D,连接BD后,得到的四边形ACDB和CEDB都是平行四边形吗?
如图,把△ABC按AC方向平移,平移的距离是AC的长度,则平移后点B平移到点D,连接BD后,得到的四边形ACDB和CEDB都是平行四边形吗?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com