
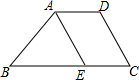
 如图,梯形ABCD的上底AD=3,下底BC=8,腰CD=4,求另一腰AB的取值范围.
如图,梯形ABCD的上底AD=3,下底BC=8,腰CD=4,求另一腰AB的取值范围. 科目:初中数学 来源: 题型:解答题
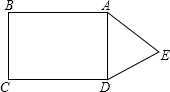 如图,这是某个小区内的道路示意图,小明家住在该小区的A处,他每天晚饭后都要从家出发随机沿着小区内的道路散步一圈后回家(每条道路不能重复走,有的道路可以不走)
如图,这是某个小区内的道路示意图,小明家住在该小区的A处,他每天晚饭后都要从家出发随机沿着小区内的道路散步一圈后回家(每条道路不能重复走,有的道路可以不走)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com