
分析 (1)由射中10环、9环、8环的概率分别是0.25、0.29、0.20,即可求得射中10环或9环的概率;
(2)由射中10环、9环、8环的概率分别是0.25、0.29、0.20,即可得不够8环的概率是:1-0.25-0.29-0.20;
(3)由(1)可得一下射中9环(包含9环)以上的次数为:100×0.54.
解答 解:(1)∵射中10环、9环、8环的概率分别是0.25、0.29、0.20,
∴射中10环或9环的概率是:0.25+0.29=0.54;
(2)∵射中10环、9环、8环的概率分别是0.25、0.29、0.20,
∴不够8环的概率是:1-0.25-0.29-0.20=0.26;
(3)一下射中9环(包含9环)以上的次数为:100×0.54=54次.
点评 此题考查了概率公式的应用.用到的知识点为:概率=所求情况数与总情况数之比.


科目:初中数学 来源: 题型:解答题
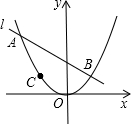 如图,已知:无论常数k为何值,直线l:y=kx+2k+2总经过定点A,若抛物线y=ax2过A,B(1,b),C(-1,c)三点.
如图,已知:无论常数k为何值,直线l:y=kx+2k+2总经过定点A,若抛物线y=ax2过A,B(1,b),C(-1,c)三点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
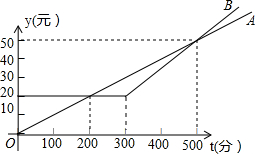 某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.
某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com