
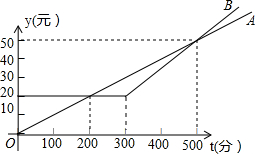
 某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.
某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600. 分析 先分别求出A,B两种手机通话套餐的函数解析式,B要分两种情况求解析式,通话费用相差5元,要分4种情况讨论:当0≤t≤200时;当200<t≤300时;当时300<t≤500;当500<t时.
解答 解:设A种手机通话套餐的函数解析式为y=mt,
把(200,20)代入y=mt得:200m=20,
解得:m=0.1,
∴A种手机通话套餐的函数解析式为y=0.1t,
当0≤t≤300时,B种手机通话套餐的函数解析式为y=20,
当t>300时,设B种手机通话套餐的函数解析式为y=kt+b,
把(300,20),(500,50)代入y=kt得:$\left\{\begin{array}{l}{300k+b=20}\\{500k+b=50}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=0.15}\\{b=-25}\end{array}\right.$,
∴B种手机通话套餐的函数解析式为y=0.15t-25,
①当0≤t≤200时,两人通话时间相同,通话费用相差5元,可得:20-0.1t=5,
解得:t=150;
②当200<t≤300时,两人通话时间相同,通话费用相差5元,可得:0.1t-20=5,
解得:t=250;
③当时300<t≤500,两人通话时间相同,通话费用相差5元,可得:0.1t-(0.15t-25)=5,
解得:t=400;
④当500<t时,两人通话时间相同,通话费用相差5元,可得:0.15t-25-0.1t=5,
解得:t=600;
∴两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.
点评 本题主要考查了一次函数的应用,解决本题的关键是求出A、B的函数解析式,然后进行分类讨论.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
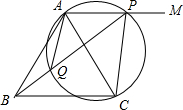 如图,等边△ABC边长为2,射线AM∥BC,P是射线AM上一动点(P不与A点重合),△APC的外接圆交BP于Q,则AQ长的最小值为( )
如图,等边△ABC边长为2,射线AM∥BC,P是射线AM上一动点(P不与A点重合),△APC的外接圆交BP于Q,则AQ长的最小值为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
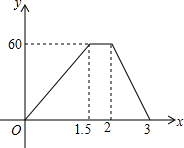 一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.
一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发x(h)时,汽车与甲地的距离为y(km),y与x的函数关系如图所示.根据图象信息解答下列问题.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com