
分析 (1)认真审题,首先根据销售方式写出一次函数关系式;
(2)根据不低于50000元,不高于52000元,写出不等式组,找出整数解;
(3)写出二元一次方程组,进而选出方案即可.
解答 解:(1)y与x之间的函数关系式:y=200x+600(200-x)=-400x+120000.
(2)由题意可得:$\left\{\begin{array}{l}-400x+120000≥50000\\-400x+120000≤52000\end{array}\right.$,
解得:170≤x≤175,
∵x为正整数,
∴x=170,171,172,173,174,175.
答:共有6种方案.
(3)假设A种化肥x吨,则B种化肥y吨.
4000x+2000y=10000,即:2x+y=5.
答:共有两种方案,A种化肥1吨,B种3吨;A种2吨,B种1吨.
点评 本题主要考查了一次函数的应用问题,以及一元一次不等式组,二元一次方程的应用,根据题意写出一次函数是解题的关键,要注意总结.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
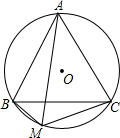 已知:⊙O是△ABC的外接圆,点M为⊙O上一点.
已知:⊙O是△ABC的外接圆,点M为⊙O上一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
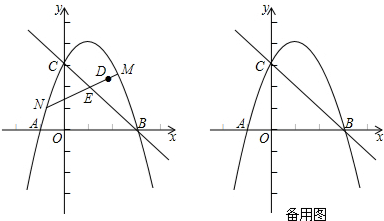
 如图,在△ABC中,AB=AC,且点A的坐标为(-3,0),点C坐标为(0,$\sqrt{3}$),点B在y轴的负半轴上,抛物线y=-$\frac{\sqrt{3}}{3}$x2+bx+c经过点A和点C
如图,在△ABC中,AB=AC,且点A的坐标为(-3,0),点C坐标为(0,$\sqrt{3}$),点B在y轴的负半轴上,抛物线y=-$\frac{\sqrt{3}}{3}$x2+bx+c经过点A和点C查看答案和解析>>
科目:初中数学 来源: 题型:填空题
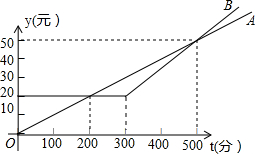 某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.
某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
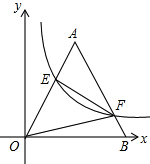 若双曲线y=$\frac{k}{x}$与边长为4的等边△AOB的边OA,AB分别相交于E,F两点,且EF⊥AE,则实数k的值为$\frac{36\sqrt{3}}{25}$.
若双曲线y=$\frac{k}{x}$与边长为4的等边△AOB的边OA,AB分别相交于E,F两点,且EF⊥AE,则实数k的值为$\frac{36\sqrt{3}}{25}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
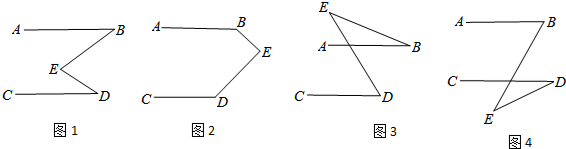
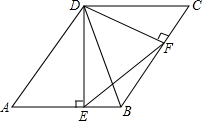 如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E、F,有下列结论:①AB=2DF;②DE•CF=DF•AE;③∠DFE=∠CDB;④如果?ABCD的面积为8,则△DEF的面积为3,其中正确结论的序号是②③④(把所有正确结论的序号填在横线上)
如图,在?ABCD中,∠A=60°,DE⊥AB,DF⊥BC,垂足分别为点E、F,有下列结论:①AB=2DF;②DE•CF=DF•AE;③∠DFE=∠CDB;④如果?ABCD的面积为8,则△DEF的面积为3,其中正确结论的序号是②③④(把所有正确结论的序号填在横线上)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com