
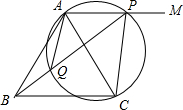
 如图,等边△ABC边长为2,射线AM∥BC,P是射线AM上一动点(P不与A点重合),△APC的外接圆交BP于Q,则AQ长的最小值为( )
如图,等边△ABC边长为2,射线AM∥BC,P是射线AM上一动点(P不与A点重合),△APC的外接圆交BP于Q,则AQ长的最小值为( )| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
分析 过点B作BD⊥直线AP,垂足为D,过点C作CE⊥直线AP,垂足为E,易得AD=AE=1,BD=CE=$\sqrt{3}$,设AP=x,则DP=x+1,EP=$|\begin{array}{l}{x-1}\end{array}|$,根据勾股定理可得BP2=x2+2x+4,CP2=x2-2x+4.易证△AQC∽△PCB,则有$\frac{AQ}{AC}$=$\frac{PC}{PB}$,由此可得AQ2=4×$\frac{{x}^{2}-2x+4}{{x}^{2}+2x+4}$,然后将该分式进行恒等变形并运用配方法就可解决问题.
方法二:探究出的Q的运动轨迹,即可解决问题.
解答 解:过点B作BD⊥直线AP,垂足为D,过点C作CE⊥直线AP,垂足为E,连接QC,如图,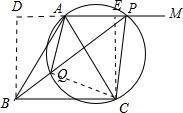
则有BD∥CE.
∵AP∥BC,∠BDE=90°,
∴四边形BCED是矩形,
∴∠DBC=∠ECB=90°.
∵△ABC是等边三角形,
∴AB=AC=BC=2,∠ABC=∠ACB=60°,
∴∠DBA=∠ECA=30°,
∴AD=1,AE=1,
∴BD=$\sqrt{3}$,CE=$\sqrt{3}$.
设AP=x,则DP=x+1,EP=$|\begin{array}{l}{x-1}\end{array}|$.
在Rt△BDP中,BP2=BD2+DP2=3+(x+1)2=x2+2x+4.
在Rt△CEP中,CP2=CE2+EP2=3+(x-1)2=x2-2x+4.
∵AM∥BC,
∴∠APB=∠CBP.
∵∠APB=∠ACQ,
∴∠ACQ=∠CBP.
∵∠QAC=∠CPB,
∴△AQC∽△PCB,
∴$\frac{AQ}{AC}$=$\frac{PC}{PB}$,
∴AQ=2×$\frac{PC}{PB}$,
∴AQ2=4×$\frac{P{C}^{2}}{P{B}^{2}}$=4×$\frac{{x}^{2}-2x+4}{{x}^{2}+2x+4}$
=4×(1-$\frac{4x}{{x}^{2}+2x+4}$)
=4×(1-$\frac{4}{x+2+\frac{4}{x}}$)
=4-$\frac{16}{(\sqrt{x}-\frac{2}{\sqrt{x}})^{2}+6}$,
当$\sqrt{x}-\frac{2}{\sqrt{x}}$=0即x=2时,AQ2取到最小值为$\frac{4}{3}$,此时AQ=$\frac{2\sqrt{3}}{3}$.
故选D.
方法二:如图,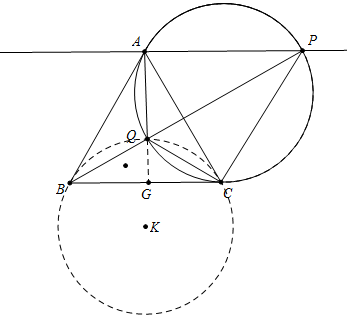
易知∠PQC=∠PAC=∠ACB=60°,
∴∠BQC=120°,
∴点Q的运动轨迹是$\widehat{BC}$,
∴当AQ⊥BC时,AQ的长最小,设AQ交BC于G,此时AG=$\sqrt{3}$,OG=$\frac{1}{2}$BQ=$\frac{1}{2}$AQ,
∴AQ的最小值为$\frac{2\sqrt{3}}{3}$,
故选D.
点评 本题主要考查了圆周角定理、平行线的性质、等边三角形的性质、矩形的判定与性质、相似三角形的判定与性质、勾股定理、30°角所对的直角边等于斜边的一半等知识,将分式进行恒等变形并运用配方法是解决本题的关键,寻找点Q的运动轨迹是方法二的突破点.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
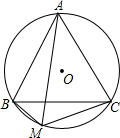 已知:⊙O是△ABC的外接圆,点M为⊙O上一点.
已知:⊙O是△ABC的外接圆,点M为⊙O上一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
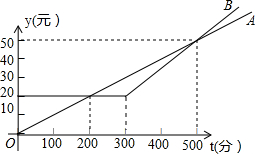 某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.
某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x<1 | B. | -1<x<1 | C. | x>-1 | D. | x<-1或x>1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com