
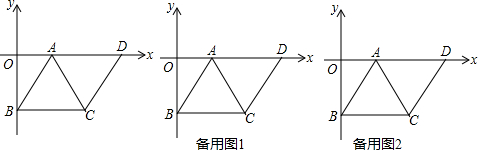
分析 (1)过点A作AH⊥于H,构造直角三角形,由勾股定理求得AH=5$\sqrt{3}$,OA=5,得到点A,B的坐标,利用待定系数法求得直线的解析式.
(2)根据点Q的不同位置,利用三角函数求得相关的线段,得到自变量的取值范围和相关的解析式.
(3)只有点Q在线段CD上时,QE才能与A垂直,由QE⊥AB,得到EQ⊥CD,因为∠ACD=60°,所以∠QNC=30°,得到CG=2(10-3t)=20-6t,AG=10-(20-6t)=6t-10,由BF=t,得到BE=2t,于是AE=10-2T,列方程2(10-2t)=6t-10,求得t=3,根据点Q到AE中点的距离大于AE的一半,所以得到点Q在圆的外面.
解答 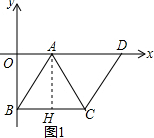 解:(1)如图1,过点A作AH⊥于H,
解:(1)如图1,过点A作AH⊥于H,
∵△ABC为等边三角形,
∴∠ABH=60°,
∵AB=10
∴AH=5$\sqrt{3}$,OA=5,
∴A(5,0),B(0,-5$\sqrt{3}$),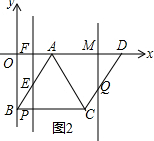
设直线AB的解析式为:y=kx+b,
∴$\left\{\begin{array}{l}{0=5k+b}\\{-5\sqrt{3}=b}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\sqrt{3}}\\{b=-5\sqrt{3}}\end{array}\right.$.
∴直线AB的解析式为:y=$\sqrt{3}$x-5$\sqrt{3}$;
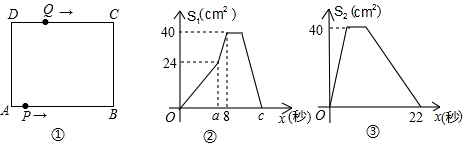
(2)如图2,由题意得:OD=15,
四边形OBPF是矩形,
∴OF=BP=t,DQ=3t,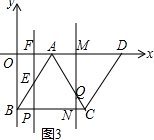
∴DM=$\frac{1}{2}$DQ=$\frac{3t}{2}$,
∴FM=15-$\frac{3t}{2}$-t=-$\frac{5t}{2}$+15,
如图3,设QM交BC于N,
∵CQ=3t-10,
∴CN=$\frac{3t-10}{2}$,
∴FM=15-5-t-($\frac{3t}{2}$-5)=-$\frac{5t}{2}$+15,
∴y=-$\frac{5t}{2}$+15(0≤t≤6),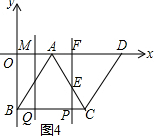 如图4,OF=BP=t,AM=$\frac{3t-20}{2}$,
如图4,OF=BP=t,AM=$\frac{3t-20}{2}$,
∴OM=5-$\frac{3t-20}{2}$,
∴FM=t-(5-$\frac{3t-20}{2}$),
即:y=$\frac{5t}{2}$-15,(6<t≤10);
(3)如图5,设QE交AC于G,
∵QE⊥AB,
∴EQ⊥CD,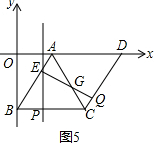
∵∠ACD=60°,
∴∠QNC=30°,
∴CG=2(10-3t)=20-6t,
∴AG=10-(20-6t)=6t-10,
∵BF=t,
∴BE=2t,
∴AE=10-2T,
∴2(10-2t)=6t-10,
∴t=3,
∴当t=3时,QE⊥AB;
∵t=3,
∴AE=4,QE=4$\sqrt{3}$>4,
∴QO′>4$\sqrt{3}$>2,
∴点Q在⊙O外.
点评 本题考查了待定系数法求函数的解析式,矩形的性质,动点问题,点与圆的位置关系,(2)中要考虑点Q的不同位置求解.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
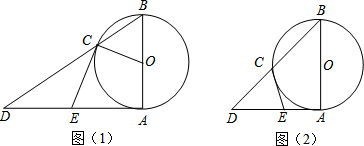
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
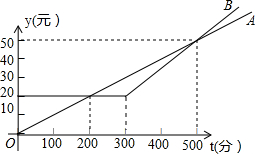 某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.
某电信公司推出了A、B两种手机通话套餐,通话费用y(元)与通话时间t(分)之间的函数关系如图所示,小明选择A套餐,小丽选择B套餐,两人通话时间相同,通话费用相差5元,则t的值为150或250或400或600.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com