
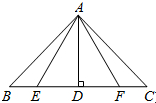
 如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )
如图所示,△ABC中,AB=AC,BE=CF,AD⊥BC,则图中共有全等三角形( )| A. | 4对 | B. | 3对 | C. | 2对 | D. | 1对 |
分析 根据等腰三角形的性质求出∠ADB=∠ADC=90°,BD=DC,根据线段垂直平分线性质求出AE=AF,求出EC=BF,再根据全等三角形的判定推出即可.
解答 解:∵AD⊥BC,AB=AC,
∴∠ADB=∠ADC=90°,BD=DC,
∵BE=CF,
∴DE=DF,
∵AD⊥BC,
∴AE=AF,
在△ADB和△ADC中,
$\left\{\begin{array}{l}{AD=AD}\\{∠ADB=∠ADC}\\{BD=DC}\end{array}\right.$,
∴△ADB≌△ADC(SAS),
同理△ADF≌△ADE,
在△AEB和△AFC中,
$\left\{\begin{array}{l}{BE=CF}\\{AE=AF}\\{AB=AC}\end{array}\right.$,
∴△AEB≌△AFC(SSS),
∵BE=CF,
∴BE+EF=CF+EF,
∴BF=CE,
在△AEC和△AFB中,
$\left\{\begin{array}{l}{EC=BF}\\{AE=AF}\\{AC=AB}\end{array}\right.$,
∴△AEC≌△AFB(SSS),
即共4对全等三角形.
故选A.
点评 本题考查了全等三角形的判定,等腰三角形的性质,线段垂直平分线性质的应用,能综合运用定理进行推理是解此题的关键,题目比较典型,难度适中.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
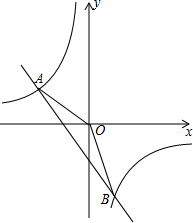 如图,已知反比例函数y1=$\frac{m}{x}$的图象与一次函数y2=kx+b的图象交于两点A(-2,1),B(a,-2).
如图,已知反比例函数y1=$\frac{m}{x}$的图象与一次函数y2=kx+b的图象交于两点A(-2,1),B(a,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
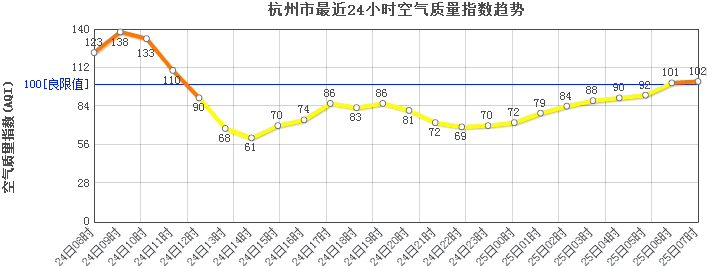
| A. | 在这个24小时中,AQI的值超过良限值时段是24日08时至24日12时 | |
| B. | 在这个24小时中,AQI对应的颜色为黄色的时段持续了20小时以上 | |
| C. | 在这个24小时中,AQI的最大值和最小值的差为77 | |
| D. | 建议中老年朋友在25日06时至07时进行晨练 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com