
 如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=6,PB=2,PC=4,求证:∠BPC=135°.
如图,△ABC中,∠ACB=90°,AC=BC,P是△ABC内一点,且PA=6,PB=2,PC=4,求证:∠BPC=135°. 分析 将△ACP绕C点逆时针旋转90°得到△BCQ,连接PQ,根据旋转的性质可得△PCQ是等腰直角三角形,BQ=PA=6,根据等腰直角三角形的性质求出PQ,∠QPC=45°,然后利用勾股定理逆定理判断出△PQB是直角三角形,∠QPB=90°,即可证明∠BPC=135°.
解答 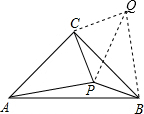 证明:将△ACP绕C点逆时针旋转90°得到△BCQ,连接PQ,
证明:将△ACP绕C点逆时针旋转90°得到△BCQ,连接PQ,
由旋转的性质可知:△PCQ是等腰直角三角形,CQ=CP=4,BQ=PA=6,
∴PQ=$\sqrt{2}$CP=4$\sqrt{2}$,且∠QPC=45°,
在△BPQ中,PB2+PQ2=4+32=36=BQ2,
∴∠QPB=90°,
∴∠BPC=∠QPB+∠QPC=135°.
点评 本题考查了旋转的性质,勾股定理的逆定理,等腰直角三角形的判定与性质,熟记各性质并作辅助线构造出等腰直角三角形和直角三角形是解题的关键.


科目:初中数学 来源: 题型:解答题
 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
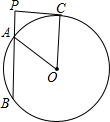 如图,PB是半径为5的圆O的一条割线,PA,PB的长是方程x2-10x+16=0的两个根(PA<PB),PC是圆O的一条切线,C是切点.则四边形PAOC的面积是14.
如图,PB是半径为5的圆O的一条割线,PA,PB的长是方程x2-10x+16=0的两个根(PA<PB),PC是圆O的一条切线,C是切点.则四边形PAOC的面积是14.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
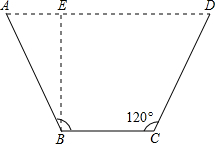 用一块宽度为5m的长方形铁片弯折成如图所示的梯形流水槽,其中BC∥AD,AB=DC,要使流水的截面面积最大,弯折的长度(AB的长)应是多少?
用一块宽度为5m的长方形铁片弯折成如图所示的梯形流水槽,其中BC∥AD,AB=DC,要使流水的截面面积最大,弯折的长度(AB的长)应是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
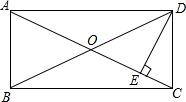 如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且DE=2$\sqrt{2}$,则AC的长是( )
如图,在矩形ABCD中,DE⊥AC于E,∠EDC:∠EDA=1:3,且DE=2$\sqrt{2}$,则AC的长是( )| A. | 4 | B. | 8 | C. | 4$\sqrt{2}$ | D. | 8$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
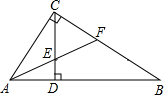 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB,交CD于E,交BC于F,若AF=BF,求证:△CEF是等边三角形.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于D,AF平分∠CAB,交CD于E,交BC于F,若AF=BF,求证:△CEF是等边三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com