
 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.分析 (1)证得DE=DF,得四边形BFDE是平行四边形,根据折叠的性质知:BF=DF,得四边形BFDE是菱形;
(2)根据折叠的性质知:AE=A′E,AB=A′D;可设AE为x,用x表示出A′E和DE的长,进而在Rt△A′DE中求出x的值,即可得到A′E的长,即可得到AE和DE长,再利用三角形的面积公式可得答案.
解答 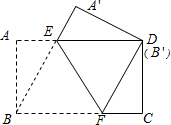 解:(1)四边形DEBF是菱形,
解:(1)四边形DEBF是菱形,
连接BE,由折叠的性质可得∠BFE=∠DFE,
∵AD∥BC,
∴∠BFE=∠DEF,
∴∠DFE=∠DEF,
∴DE=DF,
∴四边形BFDE是平行四边形,
由折叠知,BF=DF.
∴四边形BFDE是菱形;
(2)设AE=A′E=xcm,则DE=18-x;
在Rt△A′ED中,A′E=xcm,A′D=AB=12cm,ED=AD-AE=(18-x)cm;
由勾股定理得:x2+144=(18-x)2,
解得x=5;
∴S△DEF=$\frac{1}{2}$×DE×DC=$\frac{1}{2}$(18-5)×12=78(cm2).
点评 本题主要考查了勾股定理、平行四边形的判定、菱形的判定和性质,解题的关键是作好辅助线找到相关的三角形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (2,12) | B. | (2,0) | C. | (-2,12) | D. | (-2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
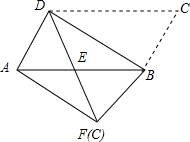 如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.
如图,将平行四边形ABCD沿对角线BD进行折叠,折叠后点C落在点F处,DF交AB于点E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com