
分析 (1)按照解方程的步骤,即可得出结论;
(2)利用换元法,令y=$\sqrt{x-3}$,解出y的值再代入y=$\sqrt{x-3}$,即可得出结论;
(3)方程两边同时乘以x2+3x-4,消去分母,解出方程后再结合原方程分母不为0验证根是否存在;
(4)利用换元法,令y=$\frac{{x}^{2}}{2x-1}$,解出y的值再代入y=$\frac{{x}^{2}}{2x-1}$,即可得出结论;
(5)结合方程2用x表示出y,代入方程1中即可求的x值,再将x值代入方程2中即可得出结论;
(6)对方程组方程编号,由①得出(x-y)2=9③;由②得出y=-x-2④,将④代入③中求出x值,在将x代入④中求出y值即可.
解答 解:(1)ax+b2=bx+a2,
移项合并同类项,得:(a+b)x=(a+b)(a-b),
解得:x=a-b.
(2)$2x+\sqrt{x-3}=6$,
移项,得:2(x-3)+$\sqrt{x-3}$=0,
令y=$\sqrt{x-3}$,则原方程变形为:,2y2+y=0,
解得:y1=0,y2=-$\frac{1}{2}$(舍去).
即$\sqrt{x-3}$=0,
解得:x=3.
(3)$\frac{4x}{{{x^2}+3x-4}}+\frac{1}{x+4}=1$,
方程两边同时乘以x2+3x-4,得:4x+x-1=x2+3x-4,
移项合并同类项,得:x2-2x-3=0,
解得:x1=1,x2=3.
当x=1时,x2+3x-4=0,故舍去,
故方程的解为:x=3.
(4)$\frac{{2{x^2}}}{2x-1}+\frac{2x-1}{x^2}-3=0$,
令y=$\frac{{x}^{2}}{2x-1}$,则原方程变形为:2y+$\frac{1}{y}$-3=0,
方程两边同时乘y,得:2y2-3y+1=0,
解得:y1=$\frac{1}{2}$,y2=1.
当$\frac{{x}^{2}}{2x-1}$=$\frac{1}{2}$时,方程无解;
当$\frac{{x}^{2}}{2x-1}$=1时,解得:x=1.
故方程的解为:x=1.
(5)$\left\{{\begin{array}{l}{4{x^2}-{y^2}=-5}\\{y-2x=1}\end{array}}\right.$,
将y=2x+1代入4x2-y2=-5中,得:4x=4,
解得:x=1,
y=2x+1=2+1=3.
故方程组的解为:$\left\{\begin{array}{l}{x=1}\\{y=3}\end{array}\right.$.
(6)$\left\{\begin{array}{l}{{x}^{2}-2xy+{y}^{2}=9①}\\{{x}^{2}+xy+2x=0②}\end{array}\right.$,
由①可得(x-y)2=9③;②可得y=-x-2④,
将④代入③中,即(2x+2)2=9,
解得:x1=$\frac{1}{2}$,x2=-$\frac{5}{2}$,
当x=$\frac{1}{2}$时,y=-$\frac{5}{2}$;
当x=-$\frac{5}{2}$时,y=$\frac{1}{2}$.
故方程组的解为:$\left\{\begin{array}{l}{x=\frac{1}{2}}\\{y=-\frac{5}{2}}\end{array}\right.$或$\left\{\begin{array}{l}{x=-\frac{5}{2}}\\{y=\frac{1}{2}}\end{array}\right.$.
点评 本题考查了解无理方程、解分式方程、解方程组以及利用换元法解方程,解题的关键是:牢记解方程的步骤,一步步得出结论.本题属于基础题,解方程是每年中考必考内容之一,这就要求同学们牢固的掌握各种解方程的方法.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 150 | |
| B. | 被抽取的150名考生 | |
| C. | 被抽取的150名考生的中考数学成绩 | |
| D. | 我市2014年中考数学成绩 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.
把一张矩形纸片(矩形ABCD)按如图方式折叠,使顶点B和点D重合,折痕为EF.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
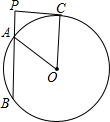 如图,PB是半径为5的圆O的一条割线,PA,PB的长是方程x2-10x+16=0的两个根(PA<PB),PC是圆O的一条切线,C是切点.则四边形PAOC的面积是14.
如图,PB是半径为5的圆O的一条割线,PA,PB的长是方程x2-10x+16=0的两个根(PA<PB),PC是圆O的一条切线,C是切点.则四边形PAOC的面积是14.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com