练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    13．如图，一个由5个大小相同、棱长为1的正方体搭成的几何体，下列关于这个几何体的说法正确的是（　　）
    A．主视图的面积为5B．左视图的面积为3C．俯视图的面积为5D．俯视图的面积为3

    分析 主视图、左视图、俯视图是分别从物体正面、左面和上面看，所得到的图形，看分别得到几个面，比较即可．

    解答 解：A、从正面看，可以看到4个正方形，面积为4，故A选项错误；
    B、从左面看，可以看到3个正方形，面积为3，故B选项正确；
    C、从上面看，可以看到4个正方形，面积为4，故C选项错误；
    D、从上面看，可以看到4个正方形，面积为4，故D选项错误．
    故选：B．

    点评 本题主要考查了几何体的三种视图面积的求法及比较，关键是掌握三视图的画法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    14．安装在屋顶的太阳能热水器的横截面示意图如图所示．已知集热管AE与支架BF所在直线相交于水箱横截面⊙O的圆心O，⊙O的半径为0.2m，AO与屋面AB的夹角为32°，与铅垂线OD的夹角为40°，BF⊥AB于B，OD⊥AD于D，AB=2m，求屋面AB的坡度和支架BF的长．（参考数据：tan18°≈$\frac{1}{3}$，tan32°≈$\frac{31}{50}$，tan40°≈$\frac{21}{25}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．观察下列图形，阅读图形下面的相关文字，

    （1）填空
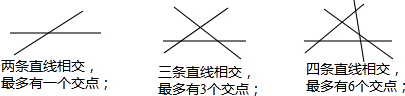
    直线条数最多交点个数对顶角的对数
    2 12
    3 36
    4 612
    51020
    …… … 
    n$\frac{n（n-1）}{2}$ n（n-1） 
    （2）当若干条直线相交时，设最多交点个数为m，对顶角对数为n，则m与n有何关系？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．如图，△ABC中，CD⊥AB，垂足为D，下列条件中：①∠A+∠B=90°；②AB2=AC2+BC2；③$\frac{AC}{AB}$=$\frac{CD}{BD}$；④CD2=AD•BD，能证明△ABC是直角三角形的有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    8．在Rt△AEB中，∠AEB=90°，以斜边AB为边向Rt△AEB形外作正方形ABCD，若正方形ABCD的对角线交于点O（如图1）
    （1）求证：EO平分∠AEB．
    （2）试猜想线段OE与EB，EA之间的数量关系，请写出结论并证明．
    （3）过点C作CF⊥EB于F，过点D作DH⊥EA于H，CF和DH的反向延长线交于点G（如图2），求证：四边形EFGH为正方形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．数学活动课上，老师提出这样一个问题：如果AB=BC，∠ABC=60°，∠APC=30°，连接PB，那么PA、PB、PC之间会有怎样的等量关系呢？经过思考后，部分同学进行了如下的交流：
    小蕾：我将图形进行了特殊化，让点P在BA延长线上（如图1），得到了一个猜想：PA2+PC2=PB2．
    小东：我假设点P在∠ABC的内部，根据题目条件，这个图形具有“共端点等线段”的特点，可以利用旋转解决问题，旋转△PAB后得到△P′CB，并且可推出△PBP′，△PCP′分别是等边三角形、直角三角形，就能得到猜想和证明方法．
    这时老师对同学们说，请大家完成以下问题：
    （1）如图2，点P在∠ABC的内部，
    ①PA=4，PC=$2\sqrt{3}$，PB=2$\sqrt{7}$．
    ②用等式表示PA、PB、PC之间的数量关系，并证明．
    （2）对于点P的其他位置，是否始终具有②中的结论？若是，请证明；若不是，请举例说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．如图的立体图形是由四个相同的小正方体组成，它的主视图是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．已知，如图，扇形AOD的半径为4，A，B，C，D是弧上四点，且AB=BC=CD=2，则AD的长度=5.5．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知，一个样本有40个数据，58，61，60，59，59；58，58，57，57，57；57，56，56，56，56；56，56，51，56，55；55，55，55，54，54；，54，54，53，53，52；52，52，52，52，51；48，49，50，50，51；
    列出频数分布表并绘制样本频数分布直方图．
    （1）计算最大值与最小值的差：13．
    （2）取组距为2，则组数为7，应分为7组．
    （3）列出频数分数表．

    查看答案和解析>>

    同步练习册答案