
【题目】如图,已知正方形ABCD的边长为4,点E、F分别在边AB,BC上,且AE=BF=1,CE,DF交于点O,下面结论:(1)∠DOC=90°;(2)OC=OE ;(3)S△ODC=S四边形BEOF.
其中正确的有____________(只填写序号)
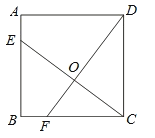
【答案】(1)(3)
【解析】
由正方形ABCD的边长为4,AE=BF=1,利用SAS易证得△EBC≌△FCD,然后全等三角形的对应角相等,易证得(1)∠DOC=90°正确;(2)由线段垂直平分线的性质与正方形的性质,可得(2)错误;由(1)易证得(3)正确.
∵正方形ABCD的边长为4,
∴BC=CD=4,∠B=∠DCF=90°,
∵AE=BF=1,
∴BE=CF=41=3,
在△EBC和△FCD中, ,
,
∴△EBC≌△FCD(SAS),
∴∠CFD=∠BEC,
∴∠BCE+∠BEC=∠BCE+∠CFD=90°,
∴∠DOC=90°;
故(1)正确;
连接DE,如图所示:
若OC=OE,
∵DF⊥EC,
∴CD=DE,
∵CD=AD<DE(矛盾),
故(2)错误;
∵△EBC≌△FCD,
∴S△EBC=S△FCD,
∴S△EBCS△FOC=S△FCDS△FOC,
即S△ODC=S四边形BEOF.
故(3)正确;
故答案为:(1)(3).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方有错误的是( )
A.x2﹣2x﹣99=0化为(x﹣1)2=100
B.x2+8x+9=0化为(x+4)2=25
C.2t2﹣7t﹣4=0化为(t﹣![]() )2=
)2=![]()
D.3x2﹣4x﹣2=0化为(x﹣![]() )2=
)2=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】朱锦汶同学学习了全等三角形后,利用全等三角形绘制出了下面系列图案,第(1)个图案由2个全等的三角形组成,第(2)个图案由4个全等的三角形组成,(3)个图案由7个全等的三角形组成,(4)个图案由12个全等的三角形组成.则第(8)个图案中全等三角形的个数为( )

A.52B.136C.256D.264
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:在坐标平面内,等腰直角![]() 中,
中,![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .
.
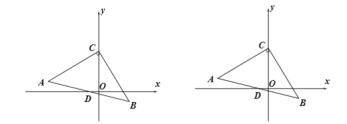
(1)求点![]() 的坐标;
的坐标;
(2)求点![]() 的坐标;
的坐标;
(3)如图,点![]() 在
在![]() 轴上,当
轴上,当![]() 的周长最小时,求出点
的周长最小时,求出点![]() 的坐标;
的坐标;
(4)在直线![]() 上有点
上有点![]() ,在
,在![]() 轴上有点
轴上有点![]() ,求出
,求出![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市推出电脑上网包月制,每月收取费用y(元)与上网时间x(小时)的函数关系如图所示,其中BA是线段,且BA∥x轴,AC是射线.
(1)当x≥30,求y与x之间的函数关系式;
(2)若小李4月份上网20小时,他应付多少元的上网费用?
(3)若小李5月份上网费用为75元,则他在该月份的上网时间是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面方法,解答后面的问题:
(阅读理解)我们已经学习了利用配方法解一元二次方程,其实配方法还有其他重要应用。
例题:已知x可取任意实数,试求二次三项式![]() 的取值范围。
的取值范围。
解: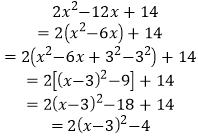
∵x取任何实数,总有![]() ,∴
,∴![]() 。
。
因此,无论x取任何实数,![]() 的值总是不小于-4的实数。
的值总是不小于-4的实数。
特别的,当x=3时,![]() 有最小值-4
有最小值-4
(应用1):已知x可取任何实数,则二次三项式![]() 的最值情况是( )
的最值情况是( )
A. 有最大值-10 B. 有最小值-10 C. 有最大值-7 D. 有最小值-7
(应用2):某品牌服装进货价为每件50元,商家在销售中发现:当以每件90元销售时,平均每天可售出20件,为了扩大销售量,增加盈利,商家决定采取适当的降价措施。
(1)将市场调查发现:如果每件服装降价1元,那么平均每天那就可多售出2件,要想平均每天销售这种服装盈利为1200元,我们设降价x元,根据题意列方程得( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
(2)请利用上面(阅读理解)提供的方法解决下面问题:
这家服装专柜为了获得每天的最大盈利,每件服装需要降价多少元?每天的最大盈利又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,AE=AF,BE与CF交于点D,则对于下列结论:①△ABE≌△ACF;②△BDF≌△CDE;③D在∠BAC的平分线上.其中正确的是( )
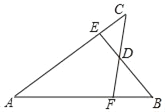
A. ① B. ② C. ①和② D. ①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了积极响应国家新农村建设,某市镇政府采用了移动宣讲的形式进行宣传动员.如图,笔直公路![]() 的一侧点
的一侧点![]() 处有一村庄,村庄
处有一村庄,村庄![]() 到公路
到公路![]() 的距离为800米,假使宣讲车
的距离为800米,假使宣讲车![]() 周围1000米以内能听到广播宣传,宣讲车
周围1000米以内能听到广播宣传,宣讲车![]() 在公路
在公路![]() 上沿
上沿![]() 方向行驶时:
方向行驶时:

(1)请问村庄能否听到宣传,并说明理由;
(2)如果能听到,已知宣讲车的速度是每分钟300米,那么村庄总共能听到多长时间的宣传?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,下列条件中不能判定直线AT是⊙O的切线的是( )
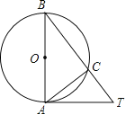
A. AB=4,AT=3,BT=5 B. ∠B=45°,AB=AT
C. ∠B=55°,∠TAC=55° D. ∠ATC=∠B
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com