
分析 先过点A作AD⊥BP于D,延长AD至点N,使得AD=ND,设ND交BC于M,连接BN,在BC上截取点Q,使得CA=CQ,连接AQ,NQ,PQ,延长CP交AQ于E,则AC=QC,∠ACP=∠BCP,进而得出AP=QP,以及AQ=BQ,再根据三角形内角和定理得到AQ=AM,∠QAM=20°,进而得出∠ABN=60°,即△ABN是等边三角形,而∠ANQ=$\frac{1}{2}$∠ANB=30°,最后根据P为△AQN的外心,得到∠APN=2∠QNA+2∠QAN=100°,进而得出△APN中,∠NAP=$\frac{1}{2}$(180°-100°)=40°,即可得到∠BAP=60°+40°=100°.
解答 解:如图所示,过点A作AD⊥BP于D,延长AD至点N,使得AD=ND,
设ND交BC于M,连接BN,在BC上截取点Q,使得CA=CQ,连接AQ,NQ,PQ,延长CP交AQ于E,则AC=QC,∠ACP=∠BCP,
∴AE=QE,CE⊥AQ,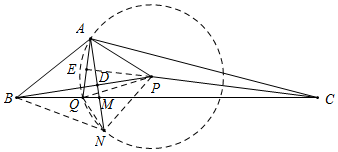
∴AP=QP,
∵△ACQ中,∠ACQ=20°,
∴∠CAE=80°,
∵∠ABQ=30°+10°=40°,∠AQC=80°,
∴∠BAQ=80°-40°=40°,
∴AQ=BQ,
∵Rt△BDM中,∠AMB=80°,
∴∠AQM=∠AMQ=80°,
∴AQ=AM,∠QAM=20°,
∴∠BAN=60°,
∵BP垂直平分AN,∠ABP=30°,
∴∠ABN=60°,即△ABN是等边三角形,
∴NB=NA,
又∵QB=QA,
∴易得△BQN≌△AQN,
∴∠ANQ=$\frac{1}{2}$∠ANB=30°,
由BP垂直平分AN,可得AP=NP,
又∵AP=QP,
∴P为△AQN的外心,
∴∠APN=2∠QNA+2∠QAN=100°,
∴△APN中,∠NAP=$\frac{1}{2}$(180°-100°)=40°,
∴∠BAP=60°+40°=100°.
点评 本题属于三角形综合题,主要考查了线段垂直平分线的性质,三角形内角和定理,圆周角定理,等边三角形的判定与性质,圆的外心以及三角形外角性质的综合应用,解决问题的关键是作辅助线构造等边三角形以及等腰三角形,依据等边三角形的性质和等腰三角形的性质进行计算求解.


科目:初中数学 来源: 题型:填空题
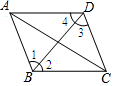 如图,有下列四个判断,其中正确的是①②③④(填写编号);
如图,有下列四个判断,其中正确的是①②③④(填写编号);查看答案和解析>>
科目:初中数学 来源: 题型:解答题
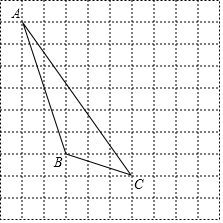 如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.
如图,在方格纸内将△ABC水平向右平移4个单位得到△A′B′C′.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
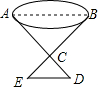 如图,要测量一池塘两端AB的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长至D,使CD=$\frac{1}{5}$CA,连接BC,并延长至E,使CE=$\frac{1}{5}$CB,连接ED,如果量出DE=25m,那么池塘宽AB等于多少?
如图,要测量一池塘两端AB的距离,可先在平地上取一个可以直接到达A和B的点C,连接AC并延长至D,使CD=$\frac{1}{5}$CA,连接BC,并延长至E,使CE=$\frac{1}{5}$CB,连接ED,如果量出DE=25m,那么池塘宽AB等于多少?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
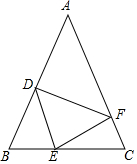 如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.
如图,在△ABC中,AB=AC,点D,E,F分别在AB,BC,AC边上,且BE=CF,BD=CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 通话时间x/min | 0<x≤5 | 5<x≤10 | 10<x≤15 | 15<x≤20 |
| 频数(通话次数) | 19 | 16 | 5 | 10 |
| A. | 0.1 | B. | 0.4 | C. | 0.5 | D. | 0.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ①② | B. | ①③ | C. | ②③ | D. | ①②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com