
【题目】在直角三角形中,除直角外的5个元素中,已知2个元素(其中至少有1个是边),就可以求出其余的3个未知元素.对于任意三角形,我们需要知道几个元素就可以求出其余的未知元素呢?思考并解答下列问题:
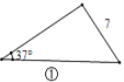

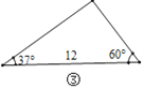
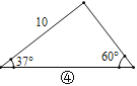
(1)观察图①~图④,根据图中三角形的已知元素,可以求出其余未知元素的序号是____.
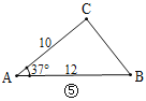
(2)如图⑤,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:
,能否求出BC的长度?如果能,请求出BC的长度;如果不能,请说明理由.(参考数据:![]() ,
,![]() ,
,![]() )
)
【答案】(1)③④;(2)能,BC=![]() .
.
【解析】
(1)①只有一个角和一条边不能求出其它元素;②只有三个角,没有已知边,不能求出其它三条边;③知道两个角和一条边,作出相应辅助线,利用三角形内角和定理、锐角三角函数及勾股定理可求出其它元素;④知道两个角和一条边,作出相应辅助线,利用三角形内角和定理、锐角三角函数及勾股定理可求出其它元素;综上即可得答案;
(2)作CD⊥AB于D,利用∠A的正弦和余弦可求出CD和AD的长,进而可求出BD的长,利用勾股定理即可求出BC的长.
(1)①只有一个角和一条边不能求出其它元素;
②只有三个角,没有已知边,不能求出其它三条边;
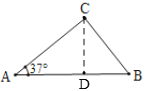
③如图,作CD⊥AB于D,
∵∠A=37°,∠B=60°,
∴∠ACB=180°-37°-60°=83°,
设AC=x,
∵∠A=37°,CD⊥AB,
∴CD=AC·sin37°=0.6x,AD=0.8x,
∵AB=12,
∴BD=12-x,
∵∠B=60°,
∴tan60°=![]() =
=![]() ,即
,即![]() ,
,
解得:x=![]() ,即AC=
,即AC=![]() .
.
∴BC=![]() =
=![]() =
=![]() .
.
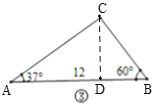
④如图,作CD⊥AB于D,
∵∠A=37°,∠B=60°,
∴∠ACB=180°-37°-60°=83°,
∵∠A=37°,CD⊥AB,AC=10,
∴CD=AC·sin37°=6,AD=AC·cos37°=8,
∵∠B=60°,
∴tan60°=![]() =
=![]() ,
,
∴BD=2![]() ,
,
∴AB=AD+BD=8+2![]() ,BC=
,BC=![]() =4
=4![]() .
.
综上所述:可以求出其余未知元素是③④,
故答案为:③④
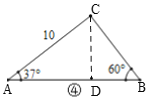
(2)如图,作CD⊥AB于D,
∴∠ADC=90°,
∵AC=10,∠A=37°,
∴CD=AC·sin37°=10×0.6=6,AD=AC·cos37°=10×0.8=8,
∵AB=12,
∴BD=12-8=4,
∴BC=![]() =
=![]() =
=![]() .
.
∴能求出BC的长,BC=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,渔船跟踪鱼群由西向东航行,到达A处时,测得小岛C位于它的北偏东53°方向,再航行![]() 后达到B处(
后达到B处(![]() ),测得小岛C位于它的北偏东45°方向.小岛C的周围
),测得小岛C位于它的北偏东45°方向.小岛C的周围![]() 内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?
内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC和点P,设点P到△ABC三边AB、AC、BC的距离分别为h1,h2,h3,△ABC的高为h.
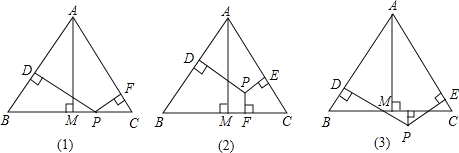
(1)若点P在一边BC上,如图①,此时h3=0,求证:h1+h2+h3=h;
(2)当点P在△ABC内,如图②,以及点P在△ABC外,如图③,这两种情况时,上述结论是否成立?若成立,请予以证明;若不成立,h1,h2,h3与h之间又有怎样的关系,请说出你的猜想,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了鼓励节能降耗,某市规定如下用电收费标准:每户每月的用电量不超过120度时,电价为a元/度;超过120度时,不超过部分仍为a元/度,超过部分为b元/度.已知某用户五月份用电115度,交电费69元,六月份用电140度,交电费94元.
(1)求a,b的值;
(2)设该用户每月用电量为x(度),应付电费为y(元);
①分别求出0≤x≤120和x>120时,y与x之间的函数关系式;
②若该用户计划七月份所付电费不超过83元,问该用户七月份最多可用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为了解旅游人数的变化情况,收集并整理了2017年1月至2019年12月期间的月接待旅游量(单位:万人次)的数据并绘制了统计图如下:
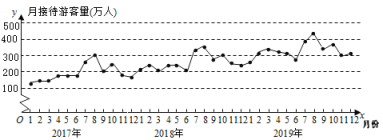
根据统计图提供的信息,下列推断不合理的是( )
A.2017年至2019年,年接待旅游量逐年增加
B.2017年至2019年,各年的月接待旅游量高峰期大致在7,8月份
C.2019年的月接待旅游量的平均值超过300万人次
D.2017年至2019年,各年下半年(7月至12月)的月接待旅游量相对于上半年(1月至6月)波动性更小,变化比较平稳
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
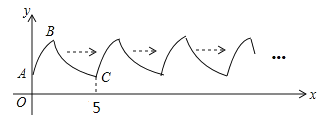
【题目】如图,曲线AB是抛物线![]() 的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线
的一部分(其中A是抛物线与y轴的交点,B是顶点),曲线BC是双曲线![]() 的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点
的一部分.曲线AB与BC组成图形W由点C开始不断重复图形W形成一组“波浪线”.若点![]() ,
,![]() 在该“波浪线”上,则m的值为________,n的最大值为________.
在该“波浪线”上,则m的值为________,n的最大值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,二次函数![]() 的图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为P.
的图象与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,顶点为P.
(1)直接写出点A,C,P的坐标.
(2)画出这个函数的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象交x轴于(-1,0)点,则下列结论中正确的是( )

A.c<0B.a-b+c<0C.b2<4acD.2a+b=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com